题目内容
9.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点与短轴的两个端点的连线互相垂直,椭圆上的点到焦点的最大距离1+$\sqrt{2}$(Ⅰ)求椭圆C的方程.
(Ⅱ)过X轴上一点M(m,0)(0<m<a)的直线l交椭圆C于A,B两点,试问:在椭圆C上是否存在定点T,使得无论直线l如何转动,以AB为直径的圆恒过定点T?若存在,求出m的值及点T的坐标,若不存在,请说明理由.
分析 (Ⅰ)运用椭圆的范围和对称性,可得b=c,a+c=1+$\sqrt{2}$,解得a,b,进而得到椭圆方程;
(Ⅱ)讨论直线l的斜率不存在,设出直线l的方程,求得圆的方程,求得定点T,讨论直线l的斜率存在,设出直线方程,联立椭圆方程,运用韦达定理和圆的性质,结合向量垂直的条件,即可得到存在定点T.
解答 解:(Ⅰ)设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F1(c,0),
依题意得:$\left\{{\begin{array}{l}{b=c}\\{a+c=1+\sqrt{2}}\\{{a^2}={b^2}+{c^2}}\end{array}}\right.$,
解得:$\left\{{\begin{array}{l}{a=\sqrt{2}}\\{b=1}\\{c=1}\end{array}}\right.$,
所以,椭圆方程为:$\frac{x^2}{2}+{y^2}=1$;
(Ⅱ)当直线l的斜率不存在时,直线l的方程为x=m,
由$\frac{m^2}{2}+{y^2}=1$,得:${y^2}=1-\frac{m^2}{2}$,
此时以AB为直径的圆的方程为:${(x-m)^2}+{y^2}=1-\frac{m^2}{2}…(1)$,
当直线l的斜率为0时,直线l的方程为y=0,
此时以AB为直径的圆的方程为:x2+y2=2…(2)
要使定点T存在,可知方程(1),(2)联立方程组只有一解,
∴$\left\{{\begin{array}{l}{x=\frac{1}{2m}+\frac{3}{4}m}\\{y=0}\end{array}}\right.$,
$\left\{{\begin{array}{l}{{{(\frac{1}{2m}+\frac{3}{4}m)}^2}=2}\\{0<m<\sqrt{2}}\end{array}}\right.$,解得$m=\frac{{\sqrt{2}}}{3}$,
所以点M的坐标为$(\frac{{\sqrt{2}}}{3},0)$时,可能椭圆上存在定点$T(\sqrt{2},0)$满足题意.
当过点$M(\frac{{\sqrt{2}}}{3},0)$直线l斜率存在时,存在定点$T(\sqrt{2},0)$满足题意,
设直线l的方程为:$x=ky+\frac{{\sqrt{2}}}{3}$,A(x1,y1),B(x2,y2),
由$\left\{{\begin{array}{l}{x=ky+\frac{{\sqrt{2}}}{3}}\\{\frac{x^2}{2}+{y^2}=1}\end{array}}\right.$,得:$({k^2}+2){y^2}+\frac{{2\sqrt{2}}}{3}ky-\frac{16}{9}=0$,
$△=\frac{8}{9}{k^2}+\frac{64}{9}({k^2}+2)>0$,${y_1}+{y_2}=-\frac{{2\sqrt{2}k}}{{3({k^2}+2)}},{y_1}•{y_2}=-\frac{16}{{9({k^2}+2)}}$,
此时,$\overrightarrow{TA}=({x_1}-\sqrt{2},{y_1}),\overrightarrow{TB}=({x_2}-\sqrt{2},{y_2})$,$\overrightarrow{TA}•\overrightarrow{TB}=({k^2}+1){y_1}{y_2}-\frac{{2\sqrt{2}}}{3}k({y_1}+{y_2})+\frac{8}{9}=({k^2}+1)[-\frac{16}{{9({k^2}+2)}}]-\frac{{2\sqrt{2}}}{3}k[-\frac{{2\sqrt{2}k}}{{3({k^2}+2)}}]+\frac{8}{9}=0$,
因此,过点$M(\frac{{\sqrt{2}}}{3},0)$直线l斜率存在时,以AB为直径的圆过定点$T(\sqrt{2},0)$.
综上所述:存在定点$T(\sqrt{2},0)$满足题意.
点评 本题考查椭圆的方程和性质,主要考查椭圆方程的运用,联立直线方程和椭圆方程,运用韦达定理,同时考查直线和圆的位置关系,考查运算能力,属于中档题.

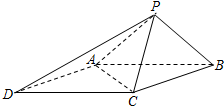 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°AB=PC=2,AP=BP=$\sqrt{2}$
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°AB=PC=2,AP=BP=$\sqrt{2}$