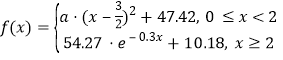题目内容
【题目】已知f（x）=3sinx﹣πx，命题p：x∈（0， 
），f（x）＜0，则（ ）
A.p是假命题，￢p：?x∈（0， ），f（x）≥0
B.p是假命题，￢p：?x0∈（0， ），f（x0）≥0
C.p是真命题，￢p：?x∈（0， ），f（x）＞0
D.p是真命题，￢p：?x0∈（0， ），f（x0）≥0
【答案】D
【解析】解：由三角函数线的性质可知，当x∈（0， 
）时，sinx＜x ∴3sinx＜3x＜πx
∴f（x）=3sinx﹣πx＜0
即命题p：x∈（0， ），f（x）＜0为真命题
根据全称命题的否定为特称命题可知￢p：x0∈（0， ），f（x0）≥0
故选D
由三角函数线的性质可知，当x∈（0， ）时，sinx＜x可判断p的真假，根据全称命题的否定为特称命题可知￢p．
练习册系列答案
相关题目
