题目内容
15.不等式ax2+bx+c>-2x的解集为{x|1<x<3}.(1)若方程ax2+bx+c+6a=0有两个相等的根,求a,b,c的值;
(2)若y=ax2+bx+c的最大值为正数,求a的取值范围.
分析 (1)根据一元二次不等式与对应方程的关系,利用判别式和根与系数的关系,即可求出a、b、c的大小.
(2)根据二次函数的最大值为正数,列出不等式,求出a的取值范围.
解答 解:(1)∵不等式ax2+bx+c>-2x的解集为{x|1<x<3},
∴方程ax2+(b+2)x+c=0的两个实数根为1、3,
且a<0;
∴1+3=-$\frac{b+2}{a}$①,1×3=$\frac{c}{a}$②;
即c=3a,b=-4a-2;
又∵方程ax2+bx+c+6a=0有两个相等的根,
∴△=b2-4a•(c+6a)=0,
即(-4a-2)2-4a•(3a+6a)=0,
化简得5a2-4a-1=0,
解得a=1(不合题意,舍),a=-$\frac{1}{5}$;
∴b=$\frac{4}{5}$-2=-$\frac{6}{5}$,c=-$\frac{3}{5}$;
(2)∵函数y=ax2+bx+c=ax2-(4a+2)x+3a,
其最大值为正数,
∴$\frac{4a•3a{-(4a+2)}^{2}}{4a}$>0,
∴4a•3a-(4a+2)2<0,
化简得a2+4a+1>0,
解得a>-2+$\sqrt{3}$,或a<-2-$\sqrt{3}$,
∴a的取值范围是{a|a<-2-$\sqrt{3}$,或-2+$\sqrt{3}$<a<0}.
点评 本题考查了一元二次不等式与对应的方程之间关系的应用问题,也考查了判别式和根与系数的关系应用问题,是综合性题目.

练习册系列答案
相关题目
6.圆锥的母线长为l,高为$\frac{1}{2}$l,则过圆锥顶点的最大截面的面积为( )
| A. | $\frac{\sqrt{3}}{4}$l2 | B. | $\frac{1}{2}$l2 | C. | $\frac{\sqrt{3}}{2}$l2 | D. | $\frac{1}{4}$l2 |
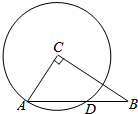 如图,已知在Rt△ABC中,∠C=90°,AC=5cm,BC=12cm,以C为圆心,CA为半径的圆交斜边于D,求AD.
如图,已知在Rt△ABC中,∠C=90°,AC=5cm,BC=12cm,以C为圆心,CA为半径的圆交斜边于D,求AD.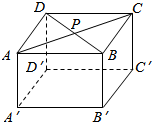 如图,在长方体ABCD-A′B′C′D′中,P是对角线AC与BD的交点,若P为四棱锥的顶点,棱锥的底面为长方体的一个面,则这样的四棱锥有( )
如图,在长方体ABCD-A′B′C′D′中,P是对角线AC与BD的交点,若P为四棱锥的顶点,棱锥的底面为长方体的一个面,则这样的四棱锥有( )