题目内容
3. 如图,矩形ABCD所在的平面和平面ABEF互相垂直,等腰梯形ABEF中,AB∥EF,
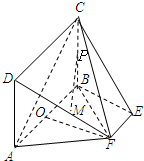
如图,矩形ABCD所在的平面和平面ABEF互相垂直,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,∠BAF=60°,O,P分别为AB,CB的中点,M为底面△OBF的重心.
(Ⅰ)求证:平面ADF⊥平面CBF;
(Ⅱ)求证:PM∥平面AFC.
分析 (Ⅰ)矩形ABCD所在的平面和平面ABEF互相垂直,CB⊥AB,所以可推断出CB⊥平面ABEF,又AF?平面BDC1,所以CB⊥AF,进而由余弦定理求得BF,推断出AF2+BF2=AB2得AF⊥BF同时利用AF∩CB=B判断出AF⊥平面CFB,即可证明平面ADF⊥平面CBF;
(Ⅱ)连结OM延长交BF于H,则H为BF的中点,又P为CB的中点,推断出PH∥CF,又利用线面判定定理推断出PH∥平面AFC,连结PO,同理推断出PO∥平面AFC,利用面面平行的判定定理,推断出平面POO1∥平面AFC,最后利用面面平行的性质推断出PM∥平面AFC
解答  证明:(Ⅰ)∵矩形ABCD所在的平面和平面ABEF互相垂直,CB⊥AB
证明:(Ⅰ)∵矩形ABCD所在的平面和平面ABEF互相垂直,CB⊥AB
∴CB⊥平面ABEF,
又AF?平面BDC1,∴CB⊥AF
又AB=2,AF=1,∠BAF=60°,
由余弦定理知BF=$\sqrt{3}$,AF2+BF2=AB2得AF⊥BF
∵AF∩CB=B,∴AF⊥平面CFB
∵AF?平面AFC,
∴平面ADF⊥平面CBF;
(Ⅱ)连结OM延长交BF于H,则H为BF的中点,又P为CB的中点,
∴PH∥CF,又∵AF?平面AFC,
∴PH∥平面AFC
连结PO,则PO∥AC,AC?平面AFC,PO∥平面AFC
PO∩PO1=P,
∴平面POO1∥平面AFC,
PM?平面AFC,
∴PM∥平面AFC.
点评 本题主要考查了面面垂直的判定,线面平行的判定,面面平行的判定,以及线面垂直的性质,属于中档题.

练习册系列答案
相关题目
14.二次函数f(x)的图象经过点(0,$\frac{3}{2}$),且f′(x)=-x-1,则不等式f(10x)>0的解集为( )
| A. | (-3,1) | B. | (-lg3,0) | C. | ($\frac{1}{1000}$,1 ) | D. | (-∞,0 ) |
18.若双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1的离心率为$\sqrt{5}$,则其渐近线方程为( )
| A. | y=±2x | B. | y=$±\sqrt{2}x$ | C. | y=$±\frac{1}{2}x$ | D. | y=$±\frac{{\sqrt{2}}}{2}x$ |
8.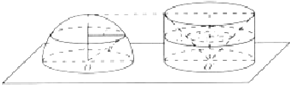 如图,取一个底面半径和高都为R的圆柱,从圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥,把所得的几何体与一个半径为R的半球放在同一水平面α上.用一平行于平面α的平面去截这两个几何体,截面分别为圆面和圆环面(图中阴影部分).设截面面积分别为S圆和S圆环,那么( )
如图,取一个底面半径和高都为R的圆柱,从圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥,把所得的几何体与一个半径为R的半球放在同一水平面α上.用一平行于平面α的平面去截这两个几何体,截面分别为圆面和圆环面(图中阴影部分).设截面面积分别为S圆和S圆环,那么( )
 如图,取一个底面半径和高都为R的圆柱,从圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥,把所得的几何体与一个半径为R的半球放在同一水平面α上.用一平行于平面α的平面去截这两个几何体,截面分别为圆面和圆环面(图中阴影部分).设截面面积分别为S圆和S圆环,那么( )
如图,取一个底面半径和高都为R的圆柱,从圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥,把所得的几何体与一个半径为R的半球放在同一水平面α上.用一平行于平面α的平面去截这两个几何体,截面分别为圆面和圆环面(图中阴影部分).设截面面积分别为S圆和S圆环,那么( )| A. | S圆>S圆环 | B. | S圆<S圆环 | C. | S圆=S圆环 | D. | 不确定 |
13.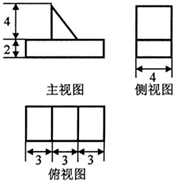 一机器元件的三视图及尺寸如图所示(单位:dm),则该组合体的体积为( )
一机器元件的三视图及尺寸如图所示(单位:dm),则该组合体的体积为( )
 一机器元件的三视图及尺寸如图所示(单位:dm),则该组合体的体积为( )
一机器元件的三视图及尺寸如图所示(单位:dm),则该组合体的体积为( )| A. | 80dm3 | B. | 88dm3 | C. | 96dm3 | D. | 112dm3 |