题目内容
18.若双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1的离心率为$\sqrt{5}$,则其渐近线方程为( )| A. | y=±2x | B. | y=$±\sqrt{2}x$ | C. | y=$±\frac{1}{2}x$ | D. | y=$±\frac{{\sqrt{2}}}{2}x$ |
分析 利用双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1的离心率为$\sqrt{5}$,可得1+$\frac{{b}^{2}}{{a}^{2}}$=5,所以$\frac{b}{a}$=2,即可求出双曲线的渐近线方程.
解答 解:因为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1的离心率为$\sqrt{5}$,
所以$\frac{c}{a}$=$\sqrt{5}$,
所以1+$\frac{{b}^{2}}{{a}^{2}}$=5,
所以$\frac{b}{a}$=2,
所以双曲线的渐近线方程为y=±2x.
故选:A.
点评 本题考查双曲线的简单性质,考查学生的计算能力,比较基础.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
6.已知$\frac{m}{1+i}$=1-ni,其中m,n∈R,i为虚数单位,则m+ni=( )
| A. | 2+i | B. | 1+2i | C. | 2-i | D. | 1-2i |
7.已知函数f(x)=sin(ωx+φ)(其中ω>0,|φ|<$\frac{π}{2}$)图象相邻对称轴的距离为$\frac{π}{2}$,一个对称轴中心为(-$\frac{π}{6}$,0),为了得到g(x)=cosx的图象,则只要将f(x)的图象( )
| A. | 向右平移$\frac{π}{6}$个单位 | B. | 向右平移$\frac{π}{12}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向左平移$\frac{π}{12}$个单位 |
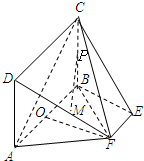 如图,矩形ABCD所在的平面和平面ABEF互相垂直,等腰梯形ABEF中,AB∥EF,
如图,矩形ABCD所在的平面和平面ABEF互相垂直,等腰梯形ABEF中,AB∥EF,