题目内容
14.二次函数f(x)的图象经过点(0,$\frac{3}{2}$),且f′(x)=-x-1,则不等式f(10x)>0的解集为( )| A. | (-3,1) | B. | (-lg3,0) | C. | ($\frac{1}{1000}$,1 ) | D. | (-∞,0 ) |
分析 先求出函数f(x)的表达式,解不等式求出x的范围即可.
解答 解:解:∵f′(x)=-x-1,
∴f(x)=-$\frac{1}{2}$x2-x+c,将(0,$\frac{3}{2}$)代入得:c=$\frac{3}{2}$,
∴f(x)=-$\frac{1}{2}$x2-x+$\frac{3}{2}$,
令f(x)>0,解得:-3<x<1,
∴-3<10x<1,解得:x<0,
故选:D.
点评 本题考查了二次函数的性质,考查了导数的应用,求出函数f(x)的表达式是解题的关键,本题属于基础题.

练习册系列答案
相关题目
9.设变量x,y满足约束条件$\left\{{\begin{array}{l}{x+y-3≥0}\\{x-y-3≤0}\\{y≥1}\end{array}}\right.$,则目标函数z=x+3y的最小值是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
2.如图所示是一个循环结构的算法,下列说法不正确的是( )
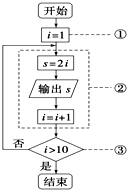

| A. | ①是循环变量初始化,循环就要开始 | |
| B. | ②为循环体 | |
| C. | ③是判断是否继续循环的终止条件 | |
| D. | 输出的S值为2,4,6,8,10,12,14,16,18 |
6.已知$\frac{m}{1+i}$=1-ni,其中m,n∈R,i为虚数单位,则m+ni=( )
| A. | 2+i | B. | 1+2i | C. | 2-i | D. | 1-2i |
4.若集合P具有以下性质:
①0∈P,1∈P; ②若x,y∈P,则x-y∈P,且x≠0时,$\frac{1}{x}$∈P.
则称集合P是“Γ集”,则下列结论不正确的是( )
①0∈P,1∈P; ②若x,y∈P,则x-y∈P,且x≠0时,$\frac{1}{x}$∈P.
则称集合P是“Γ集”,则下列结论不正确的是( )
| A. | 整数集Z是“Γ集” | |
| B. | 有理数集Q是“Γ集” | |
| C. | 对任意的一个“Γ集”P,若x,y∈P,则必有xy∈P | |
| D. | 对任意的一个“Γ集”P,若x,y∈P,且x≠0,则必有$\frac{y}{x}∈P$ |
 如图,矩形ABCD所在的平面和平面ABEF互相垂直,等腰梯形ABEF中,AB∥EF,
如图,矩形ABCD所在的平面和平面ABEF互相垂直,等腰梯形ABEF中,AB∥EF,