题目内容
12.已知函数f(x)=ax+$\frac{a-1}{x}$+1-2a(a>0),若f(x)≥lnx在[1,+∞)上恒成立,求a的取值范围.分析 把f(x)≥lnx在[1,+∞)上恒成立转化为ax+$\frac{a-1}{x}$+1-2a-lnx≥0在[1,+∞)上恒成立,然后构造函数g(x)=ax+$\frac{a-1}{x}$+1-2a-lnx,由导数分类求得函数g(x)在[1,+∞)上的最小值,由最小值大于等于0求得a的取值范围.
解答 解:由f(x)=ax+$\frac{a-1}{x}$+1-2a(a>0),f(x)≥lnx,得ax+$\frac{a-1}{x}$+1-2a-lnx≥0,
令g(x)=ax+$\frac{a-1}{x}$+1-2a-lnx,则g′(x)=$\frac{(x-1)[ax+(a-1)]}{{x}^{2}}$.
若-$\frac{a-1}{a}$=1,即a=$\frac{1}{2}$,则g′(x)≥0,函数g(x)在[1,+∞)上为增函数,又g(1)=0,
∴f(x)≥lnx在[1,+∞)上恒成立;
若-$\frac{a-1}{a}$>1,即a<$\frac{1}{2}$,当x∈(-∞,1),(-$\frac{a-1}{a}$,+∞)时,g′(x)>0,g(x)为增函数.
当x∈(1,$\frac{a-1}{a}$)时,g′(x)<0,g(x)为减函数.
∴g(x)在[1,+∞)上的最小值为g(-$\frac{a-1}{a}$).
∵g(1)=0,∴g(-$\frac{a-1}{a}$)<0,不合题意;
若-$\frac{a-1}{a}$>1,即a>$\frac{1}{2}$,当x∈(-∞,-$\frac{a-1}{a}$),(1,+∞)时,g′(x)>0,g(x)为增函数.
当x∈(-$\frac{a-1}{a}$,1)时,g′(x)<0,g(x)为减函数.
∴g(x)在[1,+∞)上的最小值为g(1).
∵g(1)=0,∴f(x)≥lnx在[1,+∞)上恒成立.
综上,a的取值范围是[$\frac{1}{2}$,+∞).
点评 本题考查了函数恒成立问题,考查了数学转化思想方法,训练了利用导数求函数的最值,体现了分类讨论的数学思想方法,是压轴题.

 习题精选系列答案
习题精选系列答案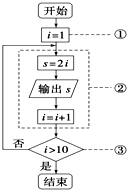
| A. | ①是循环变量初始化,循环就要开始 | |
| B. | ②为循环体 | |
| C. | ③是判断是否继续循环的终止条件 | |
| D. | 输出的S值为2,4,6,8,10,12,14,16,18 |
| A. | f(1)<f(a)<f(b) | B. | f(a)<f(b)<f(1) | C. | f(a)<f(1)<f(b) | D. | f(b)<f(1)<f(a) |
| A. | 向右平移$\frac{π}{6}$个单位 | B. | 向右平移$\frac{π}{12}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向左平移$\frac{π}{12}$个单位 |
| A. | 9 | B. | -9 | C. | -8 | D. | 8 |
①0∈P,1∈P; ②若x,y∈P,则x-y∈P,且x≠0时,$\frac{1}{x}$∈P.
则称集合P是“Γ集”,则下列结论不正确的是( )
| A. | 整数集Z是“Γ集” | |
| B. | 有理数集Q是“Γ集” | |
| C. | 对任意的一个“Γ集”P,若x,y∈P,则必有xy∈P | |
| D. | 对任意的一个“Γ集”P,若x,y∈P,且x≠0,则必有$\frac{y}{x}∈P$ |
| A. | 4π | B. | 8π | C. | 12π | D. | 16π |
| A. | $\frac{\sqrt{6}}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{2}{3}$或3 | D. | $\frac{\sqrt{6}}{2}$或$\sqrt{3}$ |
 如图,矩形ABCD所在的平面和平面ABEF互相垂直,等腰梯形ABEF中,AB∥EF,
如图,矩形ABCD所在的平面和平面ABEF互相垂直,等腰梯形ABEF中,AB∥EF,