题目内容
15.若△ABC中,b=3,∠B=$\frac{π}{3}$,则该三角形面积的最大值为$\frac{9\sqrt{3}}{4}$.分析 先表示出三角形面积,利用正弦定理换元2sinB,剩下sinAsinC,利用两角和公式化简,求得面积的最大值.
解答 解:∵$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$=$\frac{3}{\frac{\sqrt{3}}{2}}$=2$\sqrt{3}$,
∴三角形面积S=$\frac{1}{2}$acsinB=6sinAsinBsinC=3$\sqrt{3}$(sinAsinC)=$\frac{3\sqrt{3}}{2}$×[cos(A-C)-cos(A+C)]=$\frac{3\sqrt{3}}{2}$[cos(A-C)+$\frac{1}{2}$],
∴当A=C时,Smax=$\frac{9\sqrt{3}}{4}$,
故答案为:$\frac{9\sqrt{3}}{4}$.
点评 本题主要考查了正弦定理的应用,正弦定理和余弦定理是解决三角形问题常用的公式,应熟练记忆,属于中档题.

练习册系列答案
相关题目
6.已知$\frac{m}{1+i}$=1-ni,其中m,n∈R,i为虚数单位,则m+ni=( )
| A. | 2+i | B. | 1+2i | C. | 2-i | D. | 1-2i |
20.已知e是自然对数的底数,函数f(x)=ex+x-2的零点为a,函数g(x)=lnx+x-2的零点为b,则下列不等式成立的是( )
| A. | f(1)<f(a)<f(b) | B. | f(a)<f(b)<f(1) | C. | f(a)<f(1)<f(b) | D. | f(b)<f(1)<f(a) |
7.已知函数f(x)=sin(ωx+φ)(其中ω>0,|φ|<$\frac{π}{2}$)图象相邻对称轴的距离为$\frac{π}{2}$,一个对称轴中心为(-$\frac{π}{6}$,0),为了得到g(x)=cosx的图象,则只要将f(x)的图象( )
| A. | 向右平移$\frac{π}{6}$个单位 | B. | 向右平移$\frac{π}{12}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向左平移$\frac{π}{12}$个单位 |
4.若集合P具有以下性质:
①0∈P,1∈P; ②若x,y∈P,则x-y∈P,且x≠0时,$\frac{1}{x}$∈P.
则称集合P是“Γ集”,则下列结论不正确的是( )
①0∈P,1∈P; ②若x,y∈P,则x-y∈P,且x≠0时,$\frac{1}{x}$∈P.
则称集合P是“Γ集”,则下列结论不正确的是( )
| A. | 整数集Z是“Γ集” | |
| B. | 有理数集Q是“Γ集” | |
| C. | 对任意的一个“Γ集”P,若x,y∈P,则必有xy∈P | |
| D. | 对任意的一个“Γ集”P,若x,y∈P,且x≠0,则必有$\frac{y}{x}∈P$ |
5.五位同学在某次考试的数学成绩如茎叶图,则这五位同学这次考试的数学平均分为( )


| A. | 88 | B. | 89 | C. | 90 | D. | 91 |
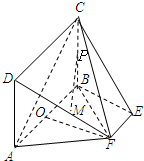 如图,矩形ABCD所在的平面和平面ABEF互相垂直,等腰梯形ABEF中,AB∥EF,
如图,矩形ABCD所在的平面和平面ABEF互相垂直,等腰梯形ABEF中,AB∥EF,