题目内容
14.设Tn是数列{an}的前n项之积,满足Tn=1-an,n∈N*;(1)证明{$\frac{1}{1{-}_{{a}_{n}}}$}是等差数列,并求出数列{an}的通项公式;
(2)设Sn=T12+T22+…+Tn2,求证:Sn>an+1-$\frac{1}{2}$.
分析 (1)通过令n=1即T1=a1=1-a1,可知a1=$\frac{1}{2}$,当n≥2时,通过Tn=1-an、an=$\frac{{T}_{n}}{{T}_{n-1}}$可知$\frac{{T}_{n}}{{T}_{n-1}}$=1-Tn,两边同除以Tn•Tn-1,可得:$\frac{1}{{T}_{n}}$-$\frac{1}{{T}_{n-1}}$=1,进而可得结论;
(2)通过an=$\frac{n}{n+1}$、累乘可知Tn=$\frac{1}{n+1}$,利用放缩法、并项相加即得结论.
解答 证明:(1)由题可知当n=1时,T1=a1=1-a1,即a1=$\frac{1}{2}$,
当n≥2时,由Tn=1-an可知an=1-Tn,
又∵an=$\frac{{T}_{n}}{{T}_{n-1}}$,
∴$\frac{{T}_{n}}{{T}_{n-1}}$=1-Tn,
两边同除以Tn•Tn-1,可得:$\frac{1}{{T}_{n}}$-$\frac{1}{{T}_{n-1}}$=1,
∴$\frac{1}{1-{a}_{n}}$-$\frac{1}{1-{a}_{n-1}}$=1,
又∵$\frac{1}{1-{a}_{1}}$=$\frac{1}{1-\frac{1}{2}}$=2,
∴数列{$\frac{1}{1{-}_{{a}_{n}}}$}是以2为首项、1为公差的等差数列,
∴$\frac{1}{1-{a}_{n}}$=2+(n-1)=n+1,
∴1-an=$\frac{1}{n+1}$,
即数列{an}的通项an=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$;
(2)∵an=$\frac{n}{n+1}$,
∴Tn=$\frac{1}{2}•\frac{2}{3}•$…$•\frac{n}{n+1}$=$\frac{1}{n+1}$,
∴Sn=T12+T22+…+Tn2
=$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{(n+1)^{2}}$
>$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{(n+1)(n+2)}$
=$\frac{1}{2}-\frac{1}{3}$+$\frac{1}{3}-\frac{1}{4}$+…+$\frac{1}{n+1}-\frac{1}{n+2}$
=$\frac{1}{2}$-$\frac{1}{n+2}$
=1-$\frac{1}{n+2}$-$\frac{1}{2}$
=$\frac{n+1}{n+2}$-$\frac{1}{2}$
=an+1-$\frac{1}{2}$.
点评 本题考查是一道数列与不等式的综合题,考查运算求解能力,注意解题方法的积累,属于中档题.

| A. | 0.3 | B. | 0.4 | C. | 0.6 | D. | 0.7 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
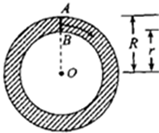 如图,我们知道圆环是线段AB绕圆心O旋转一周所形成的平面图形,所以,圆环的面积S=π(R2-r2)=(R-r)×2π×$\frac{R+r}{2}$可以看作是以线段AB=R-r为宽,以AB的中心绕圆心O旋转一周所形成的圆的周长2π×$\frac{R+r}{2}$为长的矩形面积.请将上述想法拓展到空间,并解决下列问题:若将平面区域M={(x,y)|(x-2)2+y2≤1}绕y轴旋转一周,则所形成的旋转体的体积是4π2.
如图,我们知道圆环是线段AB绕圆心O旋转一周所形成的平面图形,所以,圆环的面积S=π(R2-r2)=(R-r)×2π×$\frac{R+r}{2}$可以看作是以线段AB=R-r为宽,以AB的中心绕圆心O旋转一周所形成的圆的周长2π×$\frac{R+r}{2}$为长的矩形面积.请将上述想法拓展到空间,并解决下列问题:若将平面区域M={(x,y)|(x-2)2+y2≤1}绕y轴旋转一周,则所形成的旋转体的体积是4π2.