题目内容
16．（1）设复数z=（m-1）+（m+2）i和复平面内点Z对应，若点Z在直线2x-y=0上，求实数m的值．（2）已知z=2+i，计算$\frac{{{z^2}-4z+8}}{z-1}$．
分析 （1）根据复数对应的点在直线2x-y=0上得到m的方程解之；
（2）将z代入，化简计算．
解答 解：（1）复数z=（m-1）+（m+2）i和复平面内点Z对应，若点Z在直线2x-y=0上，
所以2（m-1）-（m+2）=0
解得m=4．
（2）z=2+i，所以$\frac{{{z^2}-4z+8}}{z-1}$=$\frac{（2+i）^{2}-4（2+i）+8}{2+i-1}$=$\frac{3}{1+i}$=$\frac{3（1-i）}{（1+i）（1-i）}$=$\frac{3-3i}{2}$=$\frac{3}{2}-\frac{3}{2}i$．
点评 本题考查了复数的几何意义以及复数的混合运算；考查学生的运算能力；属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
9．设扇形的半径长为2cm，面积为4cm2，则扇形的圆心角的弧度数是（ ）
| A． | 4 | B． | 3 | C． | 2 | D． | 1 |
7．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的一个焦点为F，以F为圆心的圆与双曲线的两条渐近线分别相切于 A、B两点，且|AB|=$\sqrt{3}$b，则该双曲线的离心率为（ ）
| A． | $\frac{{2\sqrt{3}}}{3}$ | B． | $\frac{{3\sqrt{5}}}{4}$ | C． | $2\sqrt{3}$ | D． | $\sqrt{10}$ |
4．某工厂为了调查工人文化程度与月收入的关系，随机抽取了部分工人，得到如下列表：
文化程度与月收入列联表（单位：人）
由上表中数据计算得K2=$\frac{{105×{{（{10×30-20×45}）}^2}}}{55×50×30×75}$≈6.109，请根据下表，估计有多大把握认为“文化程度与月收入有关系”（ ）
文化程度与月收入列联表（单位：人）
| 月收入2000元以下 | 月收入2000元及以上 | 总计 | |
| 高中文化以上 | 10 | 45 | 55 |
| 高中文化及以下 | 20 | 30 | 50 |
| 总计 | 30 | 75 | 105 |
| A． | 1% | B． | 99% | C． | 2.5% | D． | 97.5% |
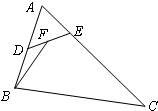如图，在△ABC中，已知AB=4，AC=6，∠BAC=60°，点D，E分别在边AB，AC上，且$\overrightarrow{AB}$=2$\overrightarrow{AD}$，$\overrightarrow{AC}$=3$\overrightarrow{AE}$，点F为DE中点，则$\overrightarrow{BF}$•$\overrightarrow{DE}$的值为（ ）
5．y=$\frac{{x}^{2}}{x+3}$的导数是（ ）
| A． | $\frac{{x}^{2}-6x}{（x+3）^{2}}$ | B． | $\frac{{x}^{2}+6x}{x+3}$ | C． | $\frac{{x}^{2}}{（x+3）^{2}}$ | D． | $\frac{{x}^{2}+6x}{（x+3）^{2}}$ |