题目内容

11．若x＞0，求y=$\frac{{x}^{2}+x+1}{x}$的最小值．

分析 y=$\frac{{x}^{2}+x+1}{x}$=x+$\frac{1}{x}$+1，利用基本不等式可得结论．

解答 解：∵x＞0，
∴y=$\frac{{x}^{2}+x+1}{x}$=x+$\frac{1}{x}$+1≥2$\sqrt{x•\frac{1}{x}}$+1=3，
当且仅当x=$\frac{1}{x}$，即x=1时，y=$\frac{{x}^{2}+x+1}{x}$的最小值为3．

点评 本题考查利用基本不等式求最小值，考查学生的计算能力，比较基础．

练习册系列答案
相关题目
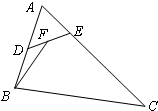1．如图，在△ABC中，已知AB=4，AC=6，∠BAC=60°，点D，E分别在边AB，AC上，且$\overrightarrow{AB}$=2$\overrightarrow{AD}$，$\overrightarrow{AC}$=3$\overrightarrow{AE}$，点F为DE中点，则$\overrightarrow{BF}$•$\overrightarrow{DE}$的值为（　　）
A．2B．3C．4D．5
2．下列四个命题：
①函数$f（x）=\frac{1}{{{x^2}-2x+2}}$的值域为（0，1]；
②若二次函数f（x）=ax2+bx+2没有零点，则b2-8a＜0且a＞0；
③函数y=x2-2|x|-3的递增区间为[1，+∞）；
④函数$y=\sqrt{x+1}•\sqrt{x-1}$和$y=\sqrt{{x^2}-1}$是相同的函数；
其中正确命题为①．
19．已知函数f（x）=a0x4+a1x3+a2x2+a3x+a4（a0，a1，a2，a3，a4∈R，且a0≠0）的四个零点构成公差为d的等差数列，则f′（x）的所有零点中最大值与最小值之差为$\sqrt{5}$|d|．
6．已知点Q（2，0）和点P（2cosα，2sinα+2），α∈[0，2π）．线段PQ的中点为M．
（Ⅰ）求点M的轨迹的参数方程；
（Ⅱ）设点P的轨迹与点M的轨迹交于A，B两点，求△QAB的面积．
16．一排九个坐位有六个人坐，若每个空位两边都坐有人，共有（　　）种不同的坐法．
A．7200B．3600C．2400D．1200
3．下列两图（图中点与年份对应）分别表示的是某市从2003年到2015年的人均生活用水量和常住人口的情况：


（Ⅰ）若从2003年到2015年中随机选择连续的三年进行观察，求所选的这三年的人均用水量恰好依次递减的概率；
（Ⅱ）由图判断，从哪年开始连续四年的常住人口的方差最大？并结合两幅图表推断该市在2012年到2015年这四年间的总生活用水量的增减情况．（结论不要求证明）
20．“m＜1”是“函数f （x）=x2-x+$\frac{1}{4}$m存在零点”的充分不必要条件．（填“充要”，“充分不必要”，“必要不充分”，“既不充分也不必要条件”）
1．已知向量$\overrightarrow a$=（-cos（π-θ），sin（-θ）），$\overrightarrow b$=（[cos（$\frac{π}{4}$-$\frac{θ}{2}$）+sin（$\frac{π}{4}$-$\frac{θ}{2}$）][cos（$\frac{π}{4}$-$\frac{θ}{2}$）-sin（$\frac{π}{4}$-$\frac{θ}{2}$）]，2cos2$\frac{θ}{2}$-1）．
（1）求证：$\overrightarrow a$⊥$\overrightarrow b$
（2）设$\overrightarrow x$=$\overrightarrow a$+（t2+3）$\overrightarrow b$，$\overrightarrow y$=-k$\overrightarrow a$+t$\overrightarrow b$，g（t）=$\frac{{k+λ{t^2}}}{t}$（λ∈[-8，0]），若存在不等于0的实数k和t（t∈[1，2]），满足$\overrightarrow x$⊥$\overrightarrow y$，试求g（t）的最小值h（λ），并求出h（λ）的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网