题目内容
12.已知数列{an}的前n项和Sn=n-5an-85(n∈N*).(1)证明数列{an-1}是等比数列并求数列{an}的通项公式;
(2)令bn=log${\;}_{\frac{5}{6}}$$\frac{1-{a}_{1}}{18}$+log${\;}_{\frac{5}{6}}$$\frac{1-{a}_{2}}{18}$+…+log${\;}_{\frac{5}{6}}$$\frac{1-{a}_{n}}{18}$,求数列{$\frac{1}{{b}_{n}}$}的前n项和Tn.
分析 (1)由Sn=n-5an-85(n∈N*).可得a1=1-5a1-85,解得a1.当n≥2时,an=Sn-Sn-1,化为6an+1=5an+1,变形为${a}_{n+1}-1=\frac{5}{6}({a}_{n-1}-1)$,利用等比数列的通项公式即可得出.
(2)由(1)可得:log${\;}_{\frac{5}{6}}$$\frac{1-{a}_{n}}{18}$=n,可得bn=$\frac{n(n+1)}{2}$.$\frac{1}{{b}_{n}}$=$2(\frac{1}{n}-\frac{1}{n+1})$.利用“裂项求和”即可得出.
解答 (1)证明:由Sn=n-5an-85(n∈N*).可得a1=1-5a1-85,解得a1=-14.
当n≥2时,an=Sn-Sn-1=n-5an-85-[(n-1)-5an-1-85],
化为6an+1=5an+1,
∴${a}_{n+1}-1=\frac{5}{6}({a}_{n-1}-1)$,
∴数列{an-1}是等比数列,首项为-15,公比为$\frac{5}{6}$,
∴${a}_{n}-1=-15×(\frac{5}{6})^{n-1}$,化为an=1-$15×(\frac{5}{6})^{n-1}$.
(2)由(1)可得:log${\;}_{\frac{5}{6}}$$\frac{1-{a}_{n}}{18}$=n,
∴bn=1+2+…+n=$\frac{n(n+1)}{2}$.
∴$\frac{1}{{b}_{n}}$=$2(\frac{1}{n}-\frac{1}{n+1})$.
∴Tn=2$[(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n}-\frac{1}{n+1})]$=2$(1-\frac{1}{n+1})$=$\frac{2n}{n+1}$.
点评 本题考查了递推式的应用、等差数列与等比数列的通项公式及前n项和公式、“裂项求和”,考查了变形能力、推理能力与计算能力,属于中档题.

| A. | -2 | B. | 2 | C. | 0 | D. | -2或0 |
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\frac{{3\sqrt{5}}}{4}$ | C. | $2\sqrt{3}$ | D. | $\sqrt{10}$ |
| A. | (0,1) | B. | (0,1] | C. | (1,+∞) | D. | [1,+∞) |
文化程度与月收入列联表(单位:人)
| 月收入2000元以下 | 月收入2000元及以上 | 总计 | |
| 高中文化以上 | 10 | 45 | 55 |
| 高中文化及以下 | 20 | 30 | 50 |
| 总计 | 30 | 75 | 105 |
| A. | 1% | B. | 99% | C. | 2.5% | D. | 97.5% |
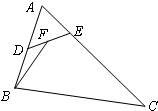 如图,在△ABC中,已知AB=4,AC=6,∠BAC=60°,点D,E分别在边AB,AC上,且$\overrightarrow{AB}$=2$\overrightarrow{AD}$,$\overrightarrow{AC}$=3$\overrightarrow{AE}$,点F为DE中点,则$\overrightarrow{BF}$•$\overrightarrow{DE}$的值为( )
如图,在△ABC中,已知AB=4,AC=6,∠BAC=60°,点D,E分别在边AB,AC上,且$\overrightarrow{AB}$=2$\overrightarrow{AD}$,$\overrightarrow{AC}$=3$\overrightarrow{AE}$,点F为DE中点,则$\overrightarrow{BF}$•$\overrightarrow{DE}$的值为( )