题目内容
14.设函数f(x)=x2+2ax-b2+4(1)若a是从0,1,2三个数中任取的一个数,b是从-2,-1,0,1,2五个数中任取的一个数,求函数f(x)有零点的概率;
(2)若a是从区间[-3,3]上任取的一个数,b是从区间[0,3]上任取的一个数,求函数g(x)=f(x)+5无零点的概率.
分析 (Ⅰ)问题等价于a2+b2≥4,列举可得基本事件共有15个,事件A包含6个基本事件,可得概率;(Ⅱ)作出图形,由几何概型的概率公式可得.
解答 解:(Ⅰ)函数f(x)=x2+2ax-b2+4有零点等价于方程x2+2ax-b2+4=0有实根,
可得△=(2a)2-4(-b2+4)≥0,可得a2+b2≥4
记事件A为函数f(x)=x2+2ax-b2+4有零点,
总的基本事件共有15个:(0,-2,),(2,-1),(2,-2),(0,-1),
(1,-1),(1,-2),(0,0),(0,1),(0,2),(1,0),(1,1),
(1,2),(2,0),(2,1),(2,2),事件A包含9个基本事件,
∴P(A)=$\frac{9}{15}=\frac{3}{5}$
(Ⅱ)如图,试验的全部结果所构成的区域为(矩形区域)
函数g(x)=f(x)+5无零点表示事件A,所构成的区域为A={(a,b)|a2+b2<9且(a,b)∈Ω}即图中的阴影部分.
∴P(A)=$\frac{\frac{1}{2}×π×9}{3×6}=\frac{π}{4}$.
点评 本题考查古典概型和几何概型,关键是首先明确概率模型,然后根据根式解答;属基础题

练习册系列答案
相关题目
2.设点M(1,y0),若在圆O:x2+y2=1上存在点N,使得∠OMN=45°,则y0的取值范围是( )
| A. | [-1,1] | B. | [-$\frac{1}{2},\frac{1}{2}$] | C. | [-$\sqrt{2},\sqrt{2}$] | D. | [-$\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}$] |
9.设扇形的半径长为2cm,面积为4cm2,则扇形的圆心角的弧度数是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
19.以下各点中,在不等式组$\left\{\begin{array}{l}{x-2y+5>0}\\{x-y+3≤0}\end{array}\right.$表示的平面区域中的点是( )
| A. | (-2,1) | B. | (2,1) | C. | (-1,2) | D. | (1,2) |
6.已知直线l1:ax-y-2=0与直线l2:$\frac{1}{2}$x-y-1=0互相垂直,则实数a的值是( )
| A. | -2 | B. | 2 | C. | 0 | D. | -2或0 |
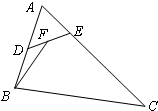 如图,在△ABC中,已知AB=4,AC=6,∠BAC=60°,点D,E分别在边AB,AC上,且$\overrightarrow{AB}$=2$\overrightarrow{AD}$,$\overrightarrow{AC}$=3$\overrightarrow{AE}$,点F为DE中点,则$\overrightarrow{BF}$•$\overrightarrow{DE}$的值为( )
如图,在△ABC中,已知AB=4,AC=6,∠BAC=60°,点D,E分别在边AB,AC上,且$\overrightarrow{AB}$=2$\overrightarrow{AD}$,$\overrightarrow{AC}$=3$\overrightarrow{AE}$,点F为DE中点,则$\overrightarrow{BF}$•$\overrightarrow{DE}$的值为( )