题目内容
2. 设M、N是直角梯形ABCD两腰的中点,DE⊥AB于E(如图),AE=EB=DE=2.现将△ADE沿DE折起,使二面角A-DE-B为90°,P,Q分别是线段AE和线段EB上任意一点,若MQ⊥PN时,求PQ长度的取值范围$[{\frac{{\sqrt{5}}}{5},1}]$.
设M、N是直角梯形ABCD两腰的中点,DE⊥AB于E(如图),AE=EB=DE=2.现将△ADE沿DE折起,使二面角A-DE-B为90°,P,Q分别是线段AE和线段EB上任意一点,若MQ⊥PN时,求PQ长度的取值范围$[{\frac{{\sqrt{5}}}{5},1}]$.
分析 先画出折叠后的图形,根据已知条件可分别以EB,ED,EA三直线为x,y,z轴,建立空间直角坐标系,并可求出图形上一些点的坐标,根据P,Q分别为线段AE、EB上的点,可设P(0,0,z),Q(x,0,0).这时可由MQ⊥PN得到$\overrightarrow{MQ}•\overrightarrow{PN}=0$,从而可得到z=1-2x,从而可以得到PQ的长度|PQ|=$\sqrt{5(x-\frac{2}{5})^{2}+\frac{1}{5}}$,这时候,根据x,z的范围可求出x的范围,由x的范围即可求出|PQ|的取值范围.
解答 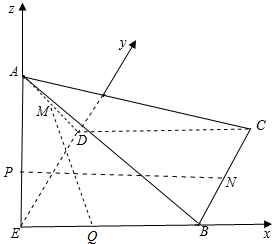 解:如图,由条件知EB,ED,EA三直线两两垂直,分别以这三直线为x,y,z轴,建立空间直角坐标系,则:
解:如图,由条件知EB,ED,EA三直线两两垂直,分别以这三直线为x,y,z轴,建立空间直角坐标系,则:
E(0,0,0),B(2,0,0),C(2,2,0),N(2,1,0),D(0,2,0),A(0,0,2),M(0,1,1);
P,Q分别是线段AE和线段EB上任意一点;
∴设P(0,0,z),Q(x,0,0),x,z∈[0,2];
∴$\overrightarrow{MQ}=(x,-1,-1)$,$\overrightarrow{PN}=(2,1,-z)$;
∵MQ⊥PN;
∴$\overrightarrow{MQ}•\overrightarrow{PN}=2x-1+z$=0;
∴z=1-2x;
∵x,z∈[0,2],∴0≤1-2x≤2;
解得$0≤x≤\frac{1}{2}$;
∴$|PQ|=\sqrt{{x}^{2}+{z}^{2}}=\sqrt{{x}^{2}+(1-2x)^{2}}$=$\sqrt{5(x-\frac{2}{5})^{2}+\frac{1}{5}}$;
∴$x=\frac{2}{5}$时,|PQ|取最小值$\sqrt{\frac{1}{5}}=\frac{\sqrt{5}}{5}$,x=0时,|PQ|取最大值$\sqrt{\frac{4}{5}+\frac{1}{5}}=1$;
∴PQ长度的取值范围为[$\frac{\sqrt{5}}{5}$,1].
故答案为:[$\frac{\sqrt{5}}{5},1$].
点评 考查二面角的大小的定义,弄清图形折叠前后的变化,建立空间直角坐标系,利用空间向量解决异面直线垂直的问题的方法,能够确定空间点的坐标,以及配方求函数最值的方法,注意正确确定变量的范围.

| A. | $\frac{2}{3}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | 2 |
| A. | 0 | B. | 1 | C. | 2 | D. | 0或2 |
| A. | 三点确定一个平面 | |
| B. | 四边形一定是平面图形 | |
| C. | 梯形一定是平面图形 | |
| D. | 两条直线没有公共点,则这两条直线平行 |
 如图,在△ABC中,AB=3$\sqrt{6}$,B=$\frac{π}{4}$,D是BC边上一点,且∠ADB=$\frac{π}{3}$.
如图,在△ABC中,AB=3$\sqrt{6}$,B=$\frac{π}{4}$,D是BC边上一点,且∠ADB=$\frac{π}{3}$.