题目内容
7．在△ABC中，若AB=3$\sqrt{2}$，AC=$\sqrt{10}$，B=45°，则边BC的长为4或2．分析 作AD⊥BC于D，首先在等腰直角三角形ABD中求得AD、BD的长，然后求得DB的长，再在直角三角形ACD中求得CD的长，再相加即可求解．
解答 
解：∵在△ABC中，由正弦定理可得：sinC=$\frac{ABsinB}{AC}$=$\frac{3\sqrt{2}×sin45°}{\sqrt{10}}$=$\frac{3\sqrt{10}}{10}$，可得：cosC=±$\sqrt{1-si{n}^{2}C}$=$±\frac{\sqrt{10}}{10}$，
∴sinA=sin（B+C）=sinBcosC+cosBsinC=$\frac{\sqrt{2}}{2}$×（$±\frac{\sqrt{10}}{10}$+$\frac{3\sqrt{10}}{10}$）=$\frac{2\sqrt{5}}{5}$或$\frac{\sqrt{5}}{5}$，
∵∠B=45°，AB=3$\sqrt{2}$，
∴由正弦定理可得：BC=$\frac{AC•sinA}{sinB}$=$\frac{\sqrt{10}×sinA}{\frac{\sqrt{2}}{2}}$=4或2．
故答案为：4或2．
点评 本题考查了等腰直角三角形的性质及勾股定理的应用，解题的关键是利用等腰直角三角形的性质求得AD、BD的长，属于基本知识的考查．
练习册系列答案
教材全解字词句篇系列答案
相关题目
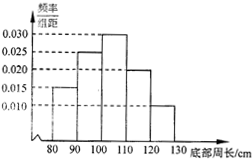为了了解一片经济林的生长情况，随机抽 测了其中80株树木的底部周长（单位：cm），所得数据均在区间[80，130]上，其频率分布直方图如图所示，则在抽测的80株树木中，有32株树木的底部周长小于100cm．
如图，在△ABC中，AB=3$\sqrt{6}$，B=$\frac{π}{4}$，D是BC边上一点，且∠ADB=$\frac{π}{3}$．
19．“指数函数y=ax（a＞1）是增函数，y=xα（α＞1）是指数函数，所以y=xα（α＞1）是增函数”，在以上演绎推理中，下列说法正确的是（ ）
| A． | 推理完全正确 | B． | 大前提不正确 | C． | 小前提不正确 | D． | 推理形式不正确 |