题目内容
9.求与圆x2+y2=5相切于点A(2,1)且过B(4,3)的圆的方程.分析 先利用待定系数法假设圆的标准方程:(x-a)2+(y-b)2=r2,求出已知圆的圆心坐标与半径,再根据条件圆C与圆x2+y2=5相切于点A(2,1)且过B(4,3),列出方程组可求相应参数,从而可求方程.
解答 解:设所求圆方程:(x-a)2+(y-b)2=r2
已知圆的圆心:(0,0),半径=$\sqrt{5}$,
由题意可得:(2-a)2+(1-b)2=r2,(4-a)2+(3-b)2=r2,a2+b2=($\sqrt{5}$+r)2,
解得a=$\frac{10}{3}$,b=$\frac{5}{3}$,r2=$\frac{20}{9}$
∴所求圆:(x-$\frac{10}{3}$)2+(y-$\frac{5}{3}$)2=$\frac{20}{9}$.
点评 本题的考点是圆的标准方程,主要考查利用待定系数法求圆的标准方程,考查学生分析解决问题的能力.

练习册系列答案
相关题目
4.若方程x2-4x-m=0的两根x1,x2,且x1-3x2=16,则m=( )
| A. | 5 | B. | -5 | C. | 21 | D. | -21 |
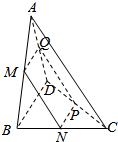 用平行于四面体ABCD的-组对棱AC和BD的平面截此四面体.得一四边形MNPQ.如图所示.
用平行于四面体ABCD的-组对棱AC和BD的平面截此四面体.得一四边形MNPQ.如图所示.