题目内容
19.已知数列{2n-1•an}的前n项和Sn=1-n2.(1)求数列{an}的通项公式;
(2)设bn=|an|n,求数列{1bn}的前n项和.
分析 (1)设bn=2n-1•an,由bn={S1,n=1Sn−Sn−1,n≥2,利用数列{2n-1•an}的前n项和Sn=1-n2,能求出bn,由此能求出数列{an}的通项公式.
(2)由已知得到bn=1n•2n,n∈N*,从而1bn=n•2n,由此利用错位相减法能求出数列{1bn}的前n项和.
解答 解:(1)设bn=2n-1•an,
∵数列{2n-1•an}的前n项和Sn=1-n2,
∴b1=S1=1-12=12,
n≥2时,bn=Sn−Sn−1=(1−n2)−(1−n−12)=-12,
∴21-1a1=b1=12,∴a1=12,
n≥2时,2n-1an=-12,∴an=-12n,
n=1时,-12n=-12≠a1,
∴an={12,n=1−12n,n≥2.
(2)∵bn=|an|n={12,n=11n•2n,n≥2=1n•2n,n∈N*,
∴1bn=n•2n,
∴数列{1bn}的前n项和:
Sn=1×2+2×22+3×23+…+n×2n,①
2Sn=1×22+2×23+3×24+…+n×2n+1,②
①-②,得:-Sn=2+22+23+…+2n-n×2n+1
=2(1−2n)1−2-n×2n+1=-2+2n+1-n×2n+1,
∴Sn=2+(n-1)×2n+1.
点评 本题考查数列的通项公式的求法,考查数列的前n项和的求法,是中档题,解题时要认真审题,注意错痊相减法的合理运用.

练习册系列答案
相关题目
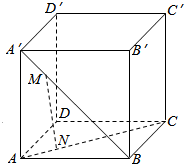 在正方体ABCD-A′B′C′D中,M,N分别是A′B,AC上的点,且A′M=AN,求证:MN∥平面BB′CC′.
在正方体ABCD-A′B′C′D中,M,N分别是A′B,AC上的点,且A′M=AN,求证:MN∥平面BB′CC′.