题目内容
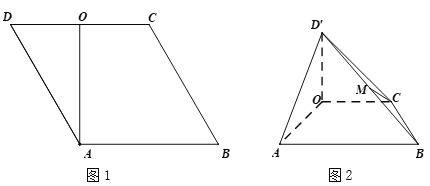
【题目】在平行四边形ABCD中,AB=1,AD![]() ,且∠BAD=45°,以BD为折线,把△ABD折起,使AB⊥DC,连接AC,得到三棱锥A﹣BCD.
,且∠BAD=45°,以BD为折线,把△ABD折起,使AB⊥DC,连接AC,得到三棱锥A﹣BCD.
(1)求证:平面ABD⊥平面BCD;
(2)求二面角B﹣AC﹣D的大小.
【答案】(1)证明见解析;(2)60°.
【解析】
(1)通过证明AB⊥平面BCD,得面面垂直;
(2)取BC中点E,过点E作EF⊥AC交AC于点F,连接DE,DF,EF,证明∠DFE为所求二面角,即可计算求解.
(1)证明:∵AB=1,AD![]() ,且∠BAD=45°,
,且∠BAD=45°,
∴BD=1,则AD2=AB2+BD2,即AB⊥BD,
又AB⊥DC,BD∩DC=D,且都在平面BCD内,
∴AB⊥平面BCD,
∵AB在平面ABD内,
∴平面ABD⊥平面BCD;

(2)取BC中点E,过点E作EF⊥AC交AC于点F,连接DE,DF,EF,
∵BD=CD=1,
∴DE⊥BC,
∵AB⊥平面BCD,DE平面BCD,
∴AB⊥DE,
∵AB∩BC=B,且都在平面ABC内,
∴DE⊥平面ABC,
∵AC平面ABC,
∴AC⊥DE,
又EF⊥AC,DE∩EF=E,且都在平面DEF内,
∴AC⊥平面DEF,
∴∠DFE为所求二面角,
在Rt△DEF中,∠DEF=90°,![]() ,
,![]() ,
,
∴ ,
,
∴∠DFE=60°,即二面角B﹣AC﹣D的大小为60°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目