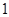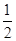题目内容
已知函数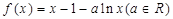 .
.
(1)若曲线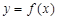 在
在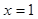 处的切线的方程为
处的切线的方程为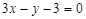 ,求实数a的值;
,求实数a的值;
(2)求证: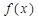 ≥0恒成立的充要条件是
≥0恒成立的充要条件是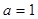 ;
;
(3)若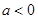 ,且对任意
,且对任意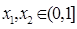 ,都有
,都有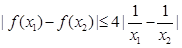 ,求实数的取值范围.
,求实数的取值范围.
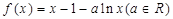 .
.(1)若曲线
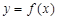 在
在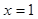 处的切线的方程为
处的切线的方程为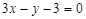 ,求实数a的值;
,求实数a的值;(2)求证:
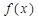 ≥0恒成立的充要条件是
≥0恒成立的充要条件是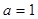 ;
;(3)若
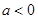 ,且对任意
,且对任意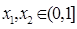 ,都有
,都有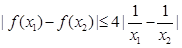 ,求实数的取值范围.
,求实数的取值范围.(1)-2;(2)见解析;(3)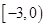 .
.
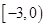 .
.(1)根据函数f(x)在x=1处的导数值为3,建立关于a的方程求出a的值.
(2)证充要条件:要从两个方面进行证明:(i)充分性.(ii)必要性.
(3)由(2)知 当a<0时,函数f(x)在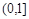 上是增函数,又函数
上是增函数,又函数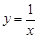 在
在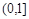 是减函数.
是减函数.
从面确定不妨设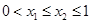 ,则
,则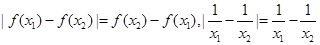 ,
,
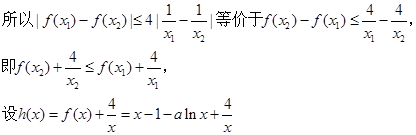
然后利用导数解决.
解: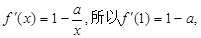 所以曲线
所以曲线 在x=1处切线的斜率为
在x=1处切线的斜率为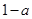 .
.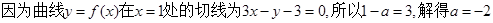 .
.
(2)①充分性
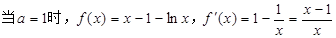
所以当
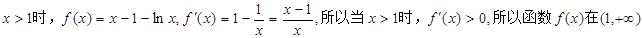 上是增函数,当
上是增函数,当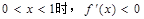 ,所以函数
,所以函数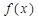 在(0,1)上是减函数,所以
在(0,1)上是减函数,所以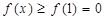
②必要性
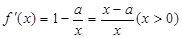
(i)当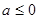 时,
时,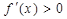 恒成立,所以函数
恒成立,所以函数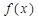 在(0,+
在(0,+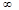 )上是增函数.而
)上是增函数.而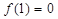 ,所以当
,所以当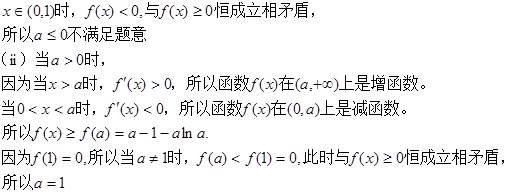
综上所述,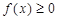 恒成立的充要条件是a=1.
恒成立的充要条件是a=1.
(3)由(2)可知
当a<0时,函数f(x)在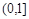 上是增函数,又函数
上是增函数,又函数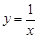 在
在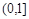 是减函数.
是减函数.
不妨设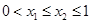 ,则
,则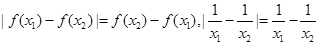

(2)证充要条件:要从两个方面进行证明:(i)充分性.(ii)必要性.
(3)由(2)知 当a<0时,函数f(x)在
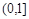 上是增函数,又函数
上是增函数,又函数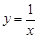 在
在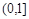 是减函数.
是减函数.从面确定不妨设
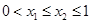 ,则
,则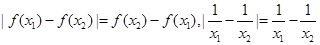 ,
,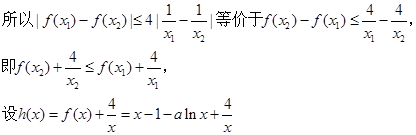
然后利用导数解决.
解:
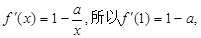 所以曲线
所以曲线 在x=1处切线的斜率为
在x=1处切线的斜率为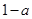 .
.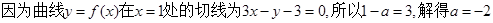 .
.(2)①充分性
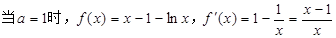
所以当
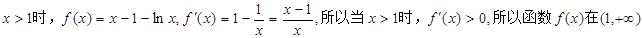 上是增函数,当
上是增函数,当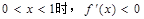 ,所以函数
,所以函数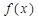 在(0,1)上是减函数,所以
在(0,1)上是减函数,所以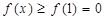
②必要性
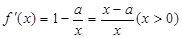
(i)当
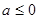 时,
时,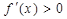 恒成立,所以函数
恒成立,所以函数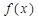 在(0,+
在(0,+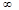 )上是增函数.而
)上是增函数.而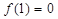 ,所以当
,所以当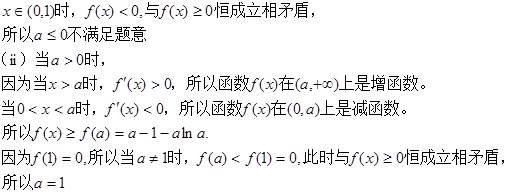
综上所述,
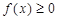 恒成立的充要条件是a=1.
恒成立的充要条件是a=1.(3)由(2)可知
当a<0时,函数f(x)在
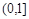 上是增函数,又函数
上是增函数,又函数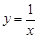 在
在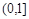 是减函数.
是减函数.不妨设
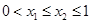 ,则
,则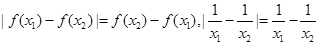


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
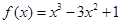 在
在 _____ 处取得极小值
_____ 处取得极小值 与
与 ,
,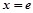 及
及 轴围成图形的面积是( )
轴围成图形的面积是( )

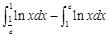

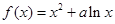 ,
,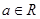 ,
,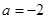 求
求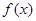 的极值
的极值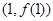 处的切线方程为
处的切线方程为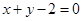 ,求实数
,求实数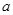 的值
的值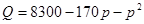 .问该商品售价定为多少元时毛利润L最大,并求最大毛利润(毛利润=销售收入-进货支出)。
.问该商品售价定为多少元时毛利润L最大,并求最大毛利润(毛利润=销售收入-进货支出)。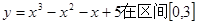 上的最大值和最小值分别是( ).
上的最大值和最小值分别是( ).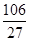
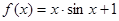 在
在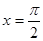 处的切线与直线
处的切线与直线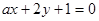 互相垂直,则实数
互相垂直,则实数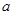 等于
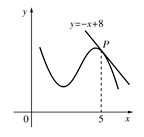
等于 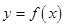 的图象在点P处的切线方程是
的图象在点P处的切线方程是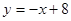 ,则
,则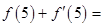 ( )
( )