题目内容

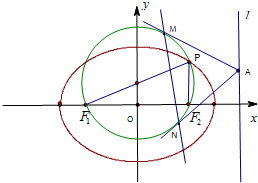
已知双曲线的方程为5x2-4y2=20两个焦点为F1，F2．
（1）求此双曲线的焦点坐标和渐近线方程；
（2）若椭圆与此双曲线有共同的焦点，且有一公共点P满足|PF1|•|PF2|=6，求椭圆的方程．
（1）双曲线的方程为5x2-4y2=20可化为
x2
4
-
y2
5
=1，
∴a=2，b=
5
，
∴c=
a2+b2
=3，
∴双曲线的焦点坐标（±3，0），渐近线方程为y=±
5
2
x；
（2）由题意，设椭圆的方程为
x2
a2
+
y2
b2
=1(a＞b＞0)，则不妨设|PF1|＞|PF2|，
∵|PF1|+|PF2|=2a，|PF1|-|PF2|=4，
∴|PF1|=a+2，|PF2|=a-2，
∵|PF1|•|PF2|=6，
∴（a+2）（a-2）=6，
∴a2=10，
∵c=3，
∴b2=1，
∴椭圆的方程为
x2
10
+y2=1．
练习册系列答案
相关题目
已知双曲线过点（3，-2），且与椭圆4x2+9y2=36有相同焦点，则双曲线的标准方程为______．
已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）经过点(
3
，-
3
2
)，且椭圆的离心率e=
1
2
，过椭圆的右焦点F作两条互相垂直的直线，分别交椭圆于点A、B及C、D．
（Ⅰ）求椭圆的方程；
（Ⅱ）求证：
1
|AB|
+
1
|CD|
为定值；
（Ⅲ）求|AB|+
9
16
|CD|的最小值．
已知双曲线C的中心在原点，焦点在x轴上，离心率为
2
，且经过点（4，-
10
）．
（Ⅰ）求双曲线C的方程；
（Ⅱ）设F1、F2为双曲线C的左、右焦点，若双曲线C上一点M满足F1M⊥F2M，求△MF1F2的面积．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0），左、右两个焦点分别为F1、F2，上顶点M（0，b），△MF1F2为正三角形且周长为6，直线l：x=my+4与椭圆C相交于A、B两点．
（Ⅰ）求椭圆C的方程；
（Ⅱ）求
OA
•
OB
的取值范围．
已知椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的左、右焦点分别是F1（-c，0）、F2（c，0），Q是椭圆外的动点，满足|
F1Q
|=2a．点P是线段F1Q与该椭圆的交点，点T在线段F2Q上，并且满足
PT
•
TF2
=0，|
TF2
|≠0．
（1）求证：|PQ|=|PF2|；
（2）求点T的轨迹C的方程；
（3）若椭圆的离心率e=
3
2
，试判断轨迹C上是否存在点M，使△F1MF2的面积S=b2，若存在，请求出∠F1MF2的正切值．
已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的左右两焦点分别为F1，F2，p是椭圆上一点，且在x轴上方，PF2⊥F1F2，PF2=λPF1，λ∈[
1
3
，
1
2
]．
（1）求椭圆的离心率e的取值范围；
（2）当e取最大值时，过F1，F2，P的圆Q的截y轴的线段长为6，求椭圆的方程；
（3）在（2）的条件下，过椭圆右准线l上任一点A引圆Q的两条切线，切点分别为M，N．试探究直线MN是否过定点？若过定点，请求出该定点；否则，请说明理由．
过点M（1，1）作一直线与椭圆
x2
9
+
y2
4
=1相交于A，B两点，若M点恰好为弦AB的中点，则AB所在直线的方程为______．
如图，椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点分别为F1，F2，离心率e=
5
5
，过F1的直线交椭圆于M、N两点，且△MNF2的周长为4
5

（Ⅰ）求椭圆E的方程；
（Ⅱ）设AB是过椭圆E中心的任意弦，P是线段AB的垂直平分线与椭圆E的一个交点，求△APB面积的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网