题目内容
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,已知曲线![]() 的参数方程为
的参数方程为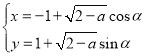 (
(![]() 为参数,
为参数,![]() ).
).
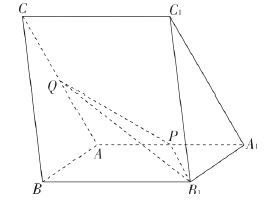
(Ⅰ)当![]() 时,若曲线
时,若曲线![]() 上存在
上存在![]() 两点关于点
两点关于点![]() 成中心对称,求直线
成中心对称,求直线![]() 的参数方程;
的参数方程;
(Ⅱ)在以原点为极点,![]() 轴正半轴为极轴的极坐标系中,极坐标方程为
轴正半轴为极轴的极坐标系中,极坐标方程为![]() 的直线
的直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,若
两点,若![]() ,求实数
,求实数![]() 的值.
的值.
【答案】见解析
【解析】(Ⅰ)由题意,得曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),
为参数),
消去参数,得![]() ,圆心
,圆心![]() 的坐标为
的坐标为![]() .……………2分
.……………2分
∵曲线![]() 上存在
上存在![]() 两点关于点
两点关于点![]() 成中心对称,
成中心对称,
∴![]() ,则由
,则由![]() ,得
,得![]() ,
,
所以直线![]() 的倾斜角为
的倾斜角为![]() ,……………4分
,……………4分
所以直线![]() 的参数方程为
的参数方程为 ,即
,即 (
(![]() 为参数).……………6分
为参数).……………6分
(Ⅱ)消去曲线![]() 的参数方程中的参数得
的参数方程中的参数得![]() ,
,
圆心![]() 为
为![]() ,半径为
,半径为![]() .……………7分
.……………7分
又直线![]() 的极坐标方程可化为
的极坐标方程可化为![]() ,……………8分
,……………8分
由![]() ,代入上式,得直线的普通方程为
,代入上式,得直线的普通方程为![]() ,
,
所以 ,∴
,∴![]() .……………10分
.……………10分
【命题意图】本题考查直线的参数方程与直角坐标方程、圆的参数方程与普通方程的互化,以及直线与圆的位置关系,意在考查逻辑推理能力、运算求解能力.

 名校课堂系列答案
名校课堂系列答案【题目】甲、乙两企业生产同一种型号零件,按规定该型号零件的质量指标值落在![]() 内为优质品.从两个企业生产的零件中各随机抽出了500件,测量这些零件的质量指标值,得结果如下表:
内为优质品.从两个企业生产的零件中各随机抽出了500件,测量这些零件的质量指标值,得结果如下表:
甲企业:

乙企业:

(1)已知甲企业的500件零件质量指标值的样本方差![]() ,该企业生产的零件质量指标值
,该企业生产的零件质量指标值![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为质量指标值的样本平均数
近似为质量指标值的样本平均数![]() (注:求
(注:求![]() 时,同一组数据用该区间的中点值作代表),
时,同一组数据用该区间的中点值作代表),![]() 近似为样本方差
近似为样本方差![]() ,试根据该企业的抽样数据,估计所生产的零件中,质量指标值不低于71.92的产品的概率.(精确到0.001)
,试根据该企业的抽样数据,估计所生产的零件中,质量指标值不低于71.92的产品的概率.(精确到0.001)
(2)由以上统计数据完成下面![]() 列联表,并问能否在犯错误的概率不超过0.01的前提下,认为“两个分厂生产的零件的质量有差异”.
列联表,并问能否在犯错误的概率不超过0.01的前提下,认为“两个分厂生产的零件的质量有差异”.

附注:
参考数据: ![]() ,
,
参考公式: ![]() ,
, ![]() ,
,
![]() .
.
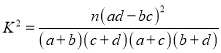
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |