题目内容
【题目】下列每组函数是同一函数的是( )
A.f(x)=x0与f(x)=1
B.f(x)= ![]() ﹣1与f(x)=|x|﹣1
﹣1与f(x)=|x|﹣1
C.f(x)= ![]() 与f(x)=x﹣2
与f(x)=x﹣2
D.f(x)= ![]() 与f(x)=
与f(x)= ![]()
【答案】B
【解析】解:对于A:f(x)=x0的定义域为{x|x≠0},而f(x)=1的定义域为R,定义域不同,∴不是同一函数;对于B:f(x)= ![]() ﹣1=|x|﹣1,的定义域为R,而f(x)=|x|﹣1的定义域为R,它们定义域相同,对应关系也相同,∴是同一函数;
﹣1=|x|﹣1,的定义域为R,而f(x)=|x|﹣1的定义域为R,它们定义域相同,对应关系也相同,∴是同一函数;
对于C:f(x)= ![]() 的定义域为{x|x≠﹣2},而与f(x)=x﹣2的定义域为R,定义域不同,∴不是同一函数;
的定义域为{x|x≠﹣2},而与f(x)=x﹣2的定义域为R,定义域不同,∴不是同一函数;
对于D:f(x)= ![]() 的定义域为{x|x≥2或x≤1},而f(x)=
的定义域为{x|x≥2或x≤1},而f(x)= ![]() 的定义域为{x|x≥2},定义域不同,∴不是同一函数;
的定义域为{x|x≥2},定义域不同,∴不是同一函数;
故选B.
【考点精析】解答此题的关键在于理解判断两个函数是否为同一函数的相关知识,掌握只有定义域和对应法则二者完全相同的函数才是同一函数.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
【题目】某家父母记录了女儿玥玥的年龄(岁)和身高(单位cm)的数据如下:
年龄x | 6 | 7 | 8 | 9 |
身高y | 118 | 126 | 136 | 144 |
(1)试求y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]()
(2)试预测玥玥10岁时的身高.(其中, ![]() =
= 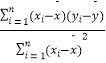 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.