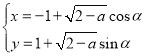��Ŀ����
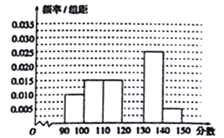
����Ŀ���ס�������ҵ����ͬһ���ͺ���������涨���ͺ����������ָ��ֵ����![]() ��Ϊ����Ʒ.��������ҵ����������и���������500����������Щ���������ָ��ֵ���ý�����±���
��Ϊ����Ʒ.��������ҵ����������и���������500����������Щ���������ָ��ֵ���ý�����±���
����ҵ��

����ҵ��

��1����֪����ҵ��500���������ָ��ֵ����������![]() ������ҵ�������������ָ��ֵ
������ҵ�������������ָ��ֵ![]() ������̬�ֲ�
������̬�ֲ�![]() ������
������![]() ����Ϊ����ָ��ֵ������ƽ����
����Ϊ����ָ��ֵ������ƽ����![]() ��ע����
��ע����![]() ʱ��ͬһ�������ø�������е�ֵ����������
ʱ��ͬһ�������ø�������е�ֵ����������![]() ����Ϊ��������
����Ϊ��������![]() ���Ը��ݸ���ҵ�ij������ݣ�����������������У�����ָ��ֵ������71.92�IJ�Ʒ�ĸ���.����ȷ��0.001��
���Ը��ݸ���ҵ�ij������ݣ�����������������У�����ָ��ֵ������71.92�IJ�Ʒ�ĸ���.����ȷ��0.001��
��2��������ͳ�������������![]() �������������ܷ��ڷ�����ĸ��ʲ�����0.01��ǰ���£���Ϊ�������ֳ�����������������в��족.
�������������ܷ��ڷ�����ĸ��ʲ�����0.01��ǰ���£���Ϊ�������ֳ�����������������в��족.

��ע��
�ο����ݣ� ![]() ��
��
�ο���ʽ�� ![]() ��
�� ![]() ��
��
![]() .
.
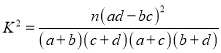
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���𰸡���1��0.159.��2��������.
�����������������
(1)���������![]() ��
�� ![]() ����ϸ��ʵ����ʿɵü���ҵ�������ָ��ֵ������71.92�IJ�Ʒ�ĸ���Ϊ0.159.
����ϸ��ʵ����ʿɵü���ҵ�������ָ��ֵ������71.92�IJ�Ʒ�ĸ���Ϊ0.159.
(2)д��������������ɵ�![]()
![]() �����ٽ�ֵ���ó����ڷ����ĸ��ʲ�����0.01��ǰ���£���Ϊ�������ֳ������IJ�Ʒ�������в��족.
�����ٽ�ֵ���ó����ڷ����ĸ��ʲ�����0.01��ǰ���£���Ϊ�������ֳ������IJ�Ʒ�������в��족.
���������
��1�������������ݣ��׳���Ʒ����ָ��ֵ��ƽ��ֵΪ��
![]()
![]() ��
��
����![]() ��
�� ![]() ��
��
������ҵ�������������ָ��ֵ![]() ������̬�ֲ�
������̬�ֲ�![]() ��
��
��![]() ����
����
![]()
![]() ��
��
![]()
![]() ��
��
���ԣ�����ҵ�������ָ��ֵ������71.92�IJ�Ʒ�ĸ���Ϊ0.159.
��2��������ͳ��������д![]() �����������£�
�����������£�

����![]()
![]()
�����ٽ�ֵ���ó����ڷ����ĸ��ʲ�����0.01��ǰ���£���Ϊ�������ֳ������IJ�Ʒ�������в��족.

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�