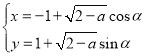题目内容
【题目】若无穷数列![]() 满足:
满足:![]() 恒等于常数
恒等于常数![]() ,则称
,则称![]() 具有局部等差数列
具有局部等差数列![]() .
.
(1)若![]() 具有局部等差数列
具有局部等差数列![]() ,且
,且![]()
![]() ,求
,求![]() ;
;
(2)若无穷数列![]() 是等差数列,无穷数列
是等差数列,无穷数列![]() 是公比为正数的等比数列,
是公比为正数的等比数列,![]() ,
,![]() ,
,![]() ,判断
,判断![]() 是否具有局部等差数列
是否具有局部等差数列![]() ,并说明理由;
,并说明理由;
(3)设![]() 既具有局部等差数列
既具有局部等差数列![]() ,又具有局部等差数列
,又具有局部等差数列![]() ,求证:
,求证:![]() 具有局部等差数列
具有局部等差数列![]() .
.
【答案】见解析
【解析】解:(1)由题意得![]() ,
, ![]() ,
,![]() ,
,![]() .
.
于是![]() ,又因为
,又因为![]() ,代入解得
,代入解得![]() .………………3分
.………………3分
(2)![]() 的公差为
的公差为![]() ,
,![]() 的公比为
的公比为![]() ,
,
所以![]() ,
,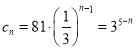 .
.
![]() .
.
![]() ,当
,当![]() 时,
时,![]() 不恒为常数,
不恒为常数,
所以![]() 不具有局部等差数列
不具有局部等差数列![]() .………………8分
.………………8分
(3)由题意得:当![]() 时
时![]() 成等差数列,
成等差数列, ![]() 也成等差数列,
也成等差数列,
所以当![]() 时
时![]()
于是当![]() 时
时![]() 成等差数列,因此
成等差数列,因此![]() (
(![]() ),
),
从而当![]() 时
时![]() 成等差数列,公差为
成等差数列,公差为![]()
由当![]() 时
时![]() ,
,
所以![]()
因此当![]() 时
时![]() 成等差数列,公差为
成等差数列,公差为![]() ,即
,即![]() 具有局部等差数列
具有局部等差数列![]() .………………16分
.………………16分
【命题意图】本题考查等差数列、等比数列的通项公式,数列单调性,反证法等基础知识,意在考查逻辑思维及推理能力、运算求解能力、分析问题解决问题的能力.

练习册系列答案
相关题目