题目内容

4．已知A（1，0），B（3，2），C（0，4），点D满足AB⊥CD，且AD∥BC，则点D的坐标为（10，-6）．

分析 由题设条件知直线AB⊥CD，且AD∥BC，将此位置关系利用斜率关系转化为方程，即可求出点D的坐标

解答 解：设点D的坐标为（x，y），由已知得，直线AB的斜率KAB=1，（2分）
直线CD的斜率KCD=$\frac{y-4}{x}$，直线CB的斜率KCB=$-\frac{2}{3}$，直线AD的斜率KAD=$\frac{y}{x-1}$，
由AB⊥CD，且AD∥BC，得$\left\{\begin{array}{l}{\frac{y-4}{x}×1=-1}\\{-\frac{2}{3}=\frac{y}{x-1}}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=10}\\{y=-6}\end{array}\right.$，
所以D的坐标为：（10，-6）．

点评 本题考点是两条直线平行、垂直与倾斜角、斜率的关系，考查用两直线垂直斜率的乘积为-1，两直线平行斜率相等（此时斜率都存在为前提），利用这一关系转化为相应的方程求坐标

练习册系列答案
相关题目
7．在△ABC中，AC=3，∠A=$\frac{π}{4}$，点D满足$\overrightarrow{CD}$=2$\overrightarrow{DB}$，且AD=$\sqrt{13}$，则BC的长为3．
8．执行如图所示的算法，则输出的结果是（　　）
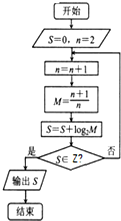
A．1B．2C．3D．4
12．711+C${\;}_{11}^{1}$•710+…+C${\;}_{11}^{10}$•7被9除以所得的余数为7．
19．设二元一次不等式组$\left\{\begin{array}{l}x+2y-19≥0\\ \;x-y+8≥0\\ 2x+y-14≤0\end{array}\right.$所表示的平面区域为M，若函数y=ax（a＞0，且a≠1）的图象经过区域M，则实数a的取值范围为[2，9]．
9．不等式|x-1|＞x-1的解集为（-∞，1）．
16．已知点M（-6，5）在双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）上，双曲线C的焦距为12，则它的渐近线方程为（　　）
A．y=±$\frac{{\sqrt{5}}}{2}$xB．y=±$\frac{{2\sqrt{5}}}{5}$xC．y=±$\frac{2}{3}$xD．y=±$\frac{3}{2}$x
13．直线l：$\left\{\begin{array}{l}{x=1-2t}\\{y=-4t}\end{array}\right.$（t为参数）与曲线C：$\left\{\begin{array}{l}{x=4cosθ}\\{y=4sinθ}\end{array}\right.$（θ为参数）公共点有2个．
14．已知椭圆γ：$\frac{x^2}{a^2}$+y2=1（常数a＞1）的左顶点为R，点A（a，1），B（-a，1），O为坐标原点．
（Ⅰ）若P是椭圆γ上任意一点，$\overrightarrow{OP}$=$m\overrightarrow{OA}$+$n\overrightarrow{OB}$，求m2+n2的值；
（Ⅱ）设M（x1，y1），N（x2，y2）是椭圆γ上的两个动点，满足kOM•kON=kOA•kOB，试探究△OMN的面积是否为定值，说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网