题目内容
8．实数x，y满足$\left\{\begin{array}{l}{y≥1}\\{y-2x+1≤0}\\{x+y-8≤0}\end{array}\right.$，则z=x-y的最小值为（ ）| A． | 2 | B． | 1 | C． | -1 | D． | -2 |
分析 由已知，画出平面区域，将目标函数变形为y=x-z的形式，求z的最小值即求直线在y轴截距的最大值．
解答 解：由已知，不等式组表示的平面区域如图，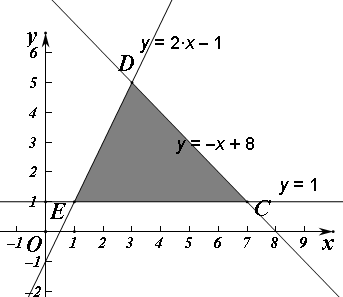
实数x，y满足的平面区域为图中阴影部分，所以当直线为y=x-z经过D时，使得-z最大，即z最小，由$\left\{\begin{array}{l}{y-2x+1=0}\\{x+y-8=0}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=3}\\{y=5}\end{array}\right.$
得到D的坐标为（3，5），
所以z=x-y的最小值为3-5=-2；
故选D．
点评 本题考查了不等式组表示的平面区域的画法以及目标函数最值的求法；关键是正确画图，找出使目标函数取最值的点．
练习册系列答案
相关题目
16．已知点M（-6，5）在双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）上，双曲线C的焦距为12，则它的渐近线方程为（ ）
| A． | y=±$\frac{{\sqrt{5}}}{2}$x | B． | y=±$\frac{{2\sqrt{5}}}{5}$x | C． | y=±$\frac{2}{3}$x | D． | y=±$\frac{3}{2}$x |
20．
如图，梯形ABCD中，AD∥BC，DC⊥BC，AD=2，BC=6，若以AB为直径的⊙O与CD相切于点E，则DE等于（ ）
如图，梯形ABCD中，AD∥BC，DC⊥BC，AD=2，BC=6，若以AB为直径的⊙O与CD相切于点E，则DE等于（ ）| A． | $\sqrt{3}$ | B． | $2\sqrt{3}$ | C． | 4 | D． | 8 |
17．某射击手射击一次命中的概率是0.7，连续两次均射中的概率是0.4，已知某次射中，则随后一次射中的概率是（ ）
| A． | $\frac{7}{10}$ | B． | $\frac{6}{7}$ | C． | $\frac{4}{7}$ | D． | $\frac{2}{5}$ |