题目内容
7.给出下列四个命题:①命题“?x∈R,x2≤0”的否定是“?x∈R,x2≤0”
②线性相关系数r的绝对值越接近于1,两个随机变量线性相关性越强;
③“x<0”是“ln(x+1)<0”的充分不必要条件;
④若随机变量ξ~N(2,1),且P(ξ>3)=0.1587,则P(ξ>1)=0.8413;
⑤命题p:f(x)=xsinx为奇函数,命题q:f(x)=cosx+1为偶函数,p∨q为假命题.
其中真命题的是( )
| A. | ①② | B. | ③④ | C. | ③⑤ | D. | ②④ |
分析 ①利用命题的否定定义,即可判断出正误;
②根据线性相关性的性质,即可判断出正误;
③利用对数函数的单调性与定义域,即可判断出正误;
④利用正态分布的对称性,即可判断出正误;
⑤利用函数的奇偶性的定义、复合命题真假的判定方法即可判断出.
解答 解:①命题“?x∈R,x2≥0”的否定是“?x∈R,x2<0”,因此不正确;
②线性相关系数r的绝对值越接近于1,表明两个随机变量线性相关性越强,正确;
③“x<0”是“ln(x+1)<0”的既不充分也不必要条件,因此不正确;
④若随机变量ξ~N(2,1),且P(ξ>3)=0.1587,则P(ξ>1)=1-P(ξ<1)=1-P(ξ>3)=0.8413,正确;
⑤命题p:f(x)=xsinx为偶函数,因此p是假命题,命题q:f(x)=cosx+1为偶函数,∴p∨q为真命题.
其中真命题的是②④.
故选:D.
点评 本题考查了简易逻辑的判定方法、概率统计的有关内容、函数的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
10.甲、乙、丙三人投掷飞镖,他们的成绩(环数)如下面的频数条形统计图所示,则甲、乙、丙三人训练成绩的方差S甲2、S乙2、S丙2的大小关系是( )
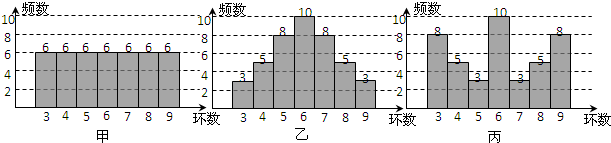

| A. | S丙2>S乙2>S甲2 | B. | S甲2>S丙2>S乙2 | C. | S丙2>S甲2>S乙2 | D. | S乙2>S丙2>S甲2 |
8.执行如图所示的算法,则输出的结果是( )


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
16.已知点M(-6,5)在双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上,双曲线C的焦距为12,则它的渐近线方程为( )
| A. | y=±$\frac{{\sqrt{5}}}{2}$x | B. | y=±$\frac{{2\sqrt{5}}}{5}$x | C. | y=±$\frac{2}{3}$x | D. | y=±$\frac{3}{2}$x |
17.某射击手射击一次命中的概率是0.7,连续两次均射中的概率是0.4,已知某次射中,则随后一次射中的概率是( )
| A. | $\frac{7}{10}$ | B. | $\frac{6}{7}$ | C. | $\frac{4}{7}$ | D. | $\frac{2}{5}$ |
 如图,多面体ABCD-A1E中,底面ABCD为正方形,AA1⊥平面ABCD,CE⊥平面ABCD,AA1=2AB=4,且CE=λAA1,A1C⊥平面BED.
如图,多面体ABCD-A1E中,底面ABCD为正方形,AA1⊥平面ABCD,CE⊥平面ABCD,AA1=2AB=4,且CE=λAA1,A1C⊥平面BED.