题目内容
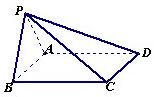
如图,在棱锥P-ABCD中,侧面PDC是边长为2的正三角形,且与底面垂直,底面ABCD是菱形,且∠ADC=60°,M为PB的中点,
(1)求证:PA⊥CD;
(2)求二面角P-AB-D的大小;
(3)求证:平面CDM⊥平面PAB.
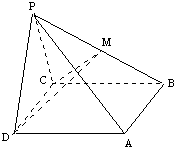
(1)求证:PA⊥CD;
(2)求二面角P-AB-D的大小;
(3)求证:平面CDM⊥平面PAB.

(1)证明,取CD中点O,连OA、OP,
∵面PCD⊥面ABCD,PO⊥CD,
∴PO⊥面ABCD,即AO为PA在面ABCD上的射影,
又在菱形ABCD中,∠ADC=60°,O为CD中点,DO=
DA,
∴AO⊥CD,由三垂线定理得,PA⊥CD.
(2)∵PA⊥CD,OA⊥CD,PA∩0A=A,∴CD⊥平面PAO,
∵AB∥CD,∴AB⊥平面PAO,∴∠PAO是二面角P-AB-D的平面角.
∵PD=AD,∴Rt△POD≌Rt△AOD,∴PO=AO,∠AOP=45°,
所以二面角P-AB-D为45°.
(3)取PA中点N,连接MN,则MN∥AB,
又AB∥CD,∴MN∥CD,
又∵N∈平面CDM,DN?平面CDM,PD=AD,∴PA⊥DN,
又∵PA⊥CD,CD∩DN=D,∴PA⊥平面CDM,
又PA?平面PAB,∴平面CDM⊥平面PAB.
∵面PCD⊥面ABCD,PO⊥CD,
∴PO⊥面ABCD,即AO为PA在面ABCD上的射影,
又在菱形ABCD中,∠ADC=60°,O为CD中点,DO=
| 1 |
| 2 |
∴AO⊥CD,由三垂线定理得,PA⊥CD.
(2)∵PA⊥CD,OA⊥CD,PA∩0A=A,∴CD⊥平面PAO,
∵AB∥CD,∴AB⊥平面PAO,∴∠PAO是二面角P-AB-D的平面角.
∵PD=AD,∴Rt△POD≌Rt△AOD,∴PO=AO,∠AOP=45°,
所以二面角P-AB-D为45°.
(3)取PA中点N,连接MN,则MN∥AB,
又AB∥CD,∴MN∥CD,
又∵N∈平面CDM,DN?平面CDM,PD=AD,∴PA⊥DN,
又∵PA⊥CD,CD∩DN=D,∴PA⊥平面CDM,
又PA?平面PAB,∴平面CDM⊥平面PAB.

练习册系列答案
相关题目
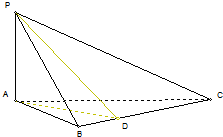
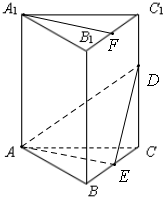
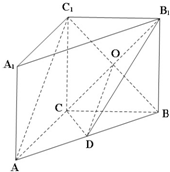
 中,
中,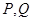 分别为线段
分别为线段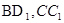 上的动点,则
上的动点,则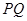 的最小值为( )
的最小值为( )