题目内容

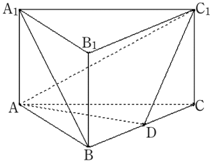
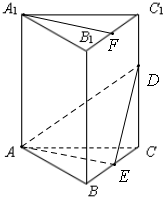
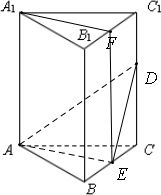
已知正三棱柱ABC-A1B1C1，D为棱CC1上任意一点，E为BC中点，F为B1C1的中点，证明：
（1）A1F∥平面ADE；
（2）平面ADE⊥平面BCC1B1．
证明：（1）连接EF，∵E、F分别为BC、B1C1的中点，∴BE∥B1F，且BE=B1F，
∴四边形BEFB1为平行四边形，
∴EF∥BB1，EF=BB1，又BB1∥AA1，BB1=AA1，
∴EF∥AA1，EF=AA1
∴四边形AEFA1为平行四边形，∴AE∥A1F，
又AE?平面ADE，A1F?平面ADE，
∴A1F∥平面ADE．
（2）∵三棱柱ABC-A1B1C1为正棱柱，∴平面ABC⊥平面BCC1B1，
∵E为BC的中点，∴AE⊥BC，
∴AE⊥平面BCC1B1，又AE?平面ADE，
∴平面ADE⊥平面BCC1B1
练习册系列答案
相关题目
△ABC所在平面外一点P，分别连接PA、PB、PC，则这四个三角形中直角三角形最多有（　　）
A．4个B．3个C．2个D．1个
如图，四棱锥S?ABCD中，底面ABCD是正方形，SA⊥面ABCD，且SA=AB，M、N分别为SB、SD中点，求证：
（1）DB∥平面AMN．
（2）SC⊥平面AMN．
如图所示，在四棱锥P-ABCD中，底面ABCD是菱形，∠BAD=60°AB=PA=2，PA⊥平面ABCD，E是PC的中点，F是AB的中点．
（1）求证：BE∥平面PDF；
（2）求证：平面PDF⊥平面PAB；
（3）求BE与平面PAC所成的角．
如图，在直三棱柱ABC-A1B1C1中，AB=AC=2AA1=2，sin∠ABC=
3
2
，D是BC的中点．
（1）求证：A1B∥平面AC1D；
（2）求证：平面AC1D⊥平面B1BCC1；
（3）求三棱锥B-AC1D的体积．
如图，在三棱锥P-ABC中，E，F分别为AC，BC的中点．
（1）求证：EF∥平面PAB；
（2）若平面PAC⊥平面ABC，且PA=PC，∠ABC=90°，求证：平面PEF⊥平面PBC．
如图，AB，CD均为圆O的直径，CE⊥圆O所在的平面，BF∥CE．求证：
（1）平面BCEF⊥平面ACE；
（2）直线DF∥平面ACE．
如图，在棱锥P-ABCD中，侧面PDC是边长为2的正三角形，且与底面垂直，底面ABCD是菱形，且∠ADC=60°，M为PB的中点，
（1）求证：PA⊥CD；
（2）求二面角P-AB-D的大小；
（3）求证：平面CDM⊥平面PAB．
如图，三棱锥A-BCD是正三棱锥，O为底面BCD的中心，以O为坐标原点，分别以OD、OA为y、z轴建立如图所示的空间直角坐标系O-xyz，若|
OA
|=|
BC
|=12，则线段AC的中点坐标是______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网