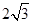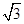题目内容
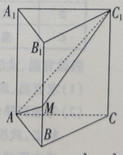
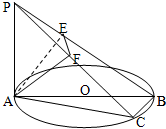
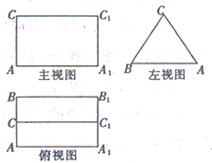
如图,在直三棱柱ABC-A1B1C1中,AC=BC,点D为AB的中点.
(1)求证:AC1∥平面CDB1;
(2)求证:平面CDB1⊥平面ABB1A1.
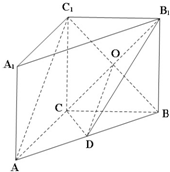
(1)求证:AC1∥平面CDB1;
(2)求证:平面CDB1⊥平面ABB1A1.

证明:(1)连接C1B交CB1于点O.
∵D,O分别是AB,C1B的中点,∴AC1∥DO,
∵AC1?平面CDB1,DO?平面CDB1,
∴AC1∥平面CDB1;
(2)∵AA1⊥底面ABC,∴AA1⊥CD
∵AC=BC,D为AB的中点,
∴CD⊥AB
∵AA1∩AB=A,
∴CD⊥平面ABB1A1,
∵CD?平面CDB1,
∴平面CDB1⊥平面ABB1A1.
∵D,O分别是AB,C1B的中点,∴AC1∥DO,
∵AC1?平面CDB1,DO?平面CDB1,
∴AC1∥平面CDB1;
(2)∵AA1⊥底面ABC,∴AA1⊥CD
∵AC=BC,D为AB的中点,
∴CD⊥AB
∵AA1∩AB=A,
∴CD⊥平面ABB1A1,
∵CD?平面CDB1,
∴平面CDB1⊥平面ABB1A1.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
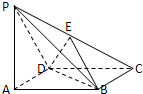
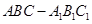 中,AB=1,BC=2,
中,AB=1,BC=2,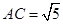 ,M为线段
,M为线段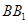 上的一动点,当
上的一动点,当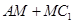 最小时,点C到平面
最小时,点C到平面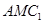 的距离为( )
的距离为( )