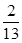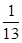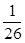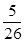题目内容
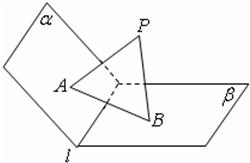
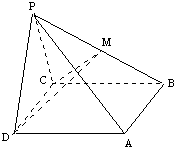
如图,已知PA⊥α,PB⊥β,垂足分别是A,B,且α∩β=l,.
(Ⅰ)求证:l⊥平面PAB;
(Ⅱ)若PA=PB=
AB,判断平面α与平面β的位置关系,并给出证明.
(Ⅰ)求证:l⊥平面PAB;
(Ⅱ)若PA=PB=
| ||
| 2 |

(Ⅰ)因为PA⊥α,l?α,所以PA⊥l,同理PB⊥l.
又PA∩PB=P,所以l⊥平面PAB.
(Ⅱ)设l与平面PAB的交点为H,连接AH,BH.
因为l⊥平面PAB,所以AH⊥l,BH⊥l,
所以∠AHB是二面角α-l-β的平面角.
又PA=PB=
AB,所以PA2+PB2=AB2,
即∠AHB=90°.
所以平面α⊥平面β.
又PA∩PB=P,所以l⊥平面PAB.
(Ⅱ)设l与平面PAB的交点为H,连接AH,BH.
因为l⊥平面PAB,所以AH⊥l,BH⊥l,
所以∠AHB是二面角α-l-β的平面角.
又PA=PB=
| ||
| 2 |
即∠AHB=90°.
所以平面α⊥平面β.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
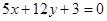 与
与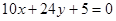 的距离是( )
的距离是( )