题目内容
【题目】某公司为感谢全体员工的辛勤劳动，决定在年终答谢会上，通过摸球方式对全公司1000位员工进行现金抽奖。规定：每位员工从装有4个相同质地球的袋子中一次性随机摸出2个球，这4个球上分别标有数字
、
、
、
，摸出来的两个球上的数字之和为该员工所获的奖励额
（单位：元）。公司拟定了以下三个数字方案：
方案 |
|
|
|
|
一 | 100 | 100 | 100 | 500 |
二 | 100 | 100 | 500 | 500 |
三 | 200 | 200 | 400 | 400 |
（Ⅰ）如果采取方案一，求
的概率；
（Ⅱ）分别计算方案二、方案三的平均数
和方差
，如果要求员工所获的奖励额相对均衡，方案二和方案三选择哪个更好？
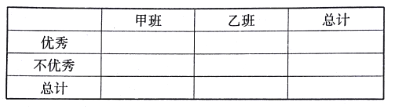
（Ⅲ）在投票选择方案二还是方案三时，公司按性别分层抽取100名员工进行统计，得到如下不完整的
列联表。请将该表补充完整，并判断能否有90%的把握认为“选择方案二或方案三与性别有关”？
方案二 | 方案三 | 合计 | |
男性 | 12 | ||
女性 | 40 | ||
合计 | 82 | 100 |
附：
| 0.15 | 0.10 | 0.05 |
| 2.072 | 2.706 | 3.841 |
【答案】（1）
（2）选择方案三较好（3）不能
【解析】试题分析：（Ⅰ）利用枚举法，写出所有的基本事件，找出其中方案一包含的基本事件上，再利用古典概型可求得概率；（Ⅱ）由已知数据，结合平均数与方差的的计算公式可求得结果；（Ⅲ）利用所给条件，填好列联表，求出常数
，结合独立性检验及所给数据得出判断．
试题解析：（Ⅰ）从a、b、c、d中取两个，共有ab、ac、ad、bc、bd、cd 这6个基本事件
采取方案一，设
为事件A，它包含ab、ac、bc这3个基本事件
由于每个基本事件都是等可能的，所以
（Ⅱ）依题意，求数据ab、ac、ad、bc、bd、cd的平均数
和方差
。
,
,
,
,
，
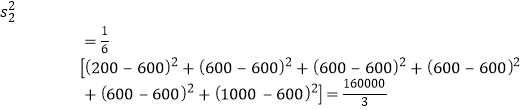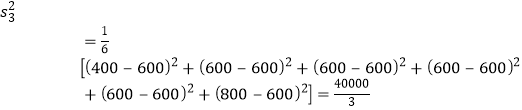，方案三的方差较小，相对均衡，选择方案三较好。
二 | 三 | 合计 | |
男性 | 12 | 48 | 60 |
女性 | 6 | 34 | 40 |
合计 | 18 | 82 | 100 |
（Ⅲ）
直接计算得，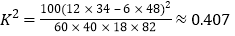
，
，
所以不能以
的把握认为选择方案二或三与性别有关。
