题目内容
【题目】设函数![]()
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)如果不等式![]() 对于一切的
对于一切的![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)证明:不等式![]() 对于一切的
对于一切的![]() 恒成立.
恒成立.
【答案】(1)![]() (2)
(2)![]() (3)见解析
(3)见解析
【解析】分析:(1)先求一阶导函数![]() ,
,![]() ,用点斜式写出切线方程。
,用点斜式写出切线方程。
(2)分离变量![]() ,
,![]() ,构建函数
,构建函数![]() ,转化为求函数
,转化为求函数![]() 的最大值
的最大值
(3)构建函数![]() ,证明
,证明![]() 的最小值大于0.
的最小值大于0.
解:(1)当![]() 时,
时,![]() ,则
,则![]() ,故
,故![]() ,所以曲线
,所以曲线![]() 在点
在点![]() 处的切线方程为:
处的切线方程为:![]() ;
;
(2)因为![]() ,所以
,所以![]() 恒成立,等价于
恒成立,等价于![]() 恒成立.
恒成立.
设![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,所以
,所以 ![]() 在
在![]() 上单调递减,
上单调递减,
所以 ![]() 时,
时,![]() .
.
因为 ![]() 恒成立,所以
恒成立,所以![]() 的取值范围是
的取值范围是![]() ;
;
(3)当![]() 时,
时,![]() ,等价于
,等价于![]() .
.
设![]() ,
,![]() ,得
,得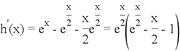 .
.
由(2)可知,![]() 时,
时,![]() 恒成立.
恒成立.
所以![]() 时,
时,![]() ,有
,有![]() ,所以
,所以![]() .
.
所以![]() 在
在![]() 上单调递增,当
上单调递增,当![]() 时,
时,![]() .
.
因此当![]() 时,
时,![]() 恒成立
恒成立
分析:(1)利用导数求在某点![]() 切线方程利用
切线方程利用![]() ,
,![]() 即可。
即可。
(2)已知不等式的恒成立,求解参数的取值范围,分离变量,转化为求函数的最值问题。
(3)证明不等式![]() 恒成立问题,构建函数
恒成立问题,构建函数![]() ,证明
,证明![]() 的最小值大于0.
的最小值大于0.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
【题目】某中学将100名髙一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师对甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如下图).记成绩不低于90分者为“成绩优秀”

| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(I)从乙班随机抽取2名学生的成绩,记“成绩优秀”的个数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(II)根据频率分布直方图填写下面2 x2列联表,并判断是否有95%的把握认为:“成绩优秀”与教学方式有关.
甲班(A方式) | 乙班(B方式) | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
附: 
