题目内容
7．若复数z满足（4-3i）z=|3+4i|，则z的虚部为（ ）| A． | $\frac{3}{5}$i | B． | $\frac{3}{5}$ | C． | 3 | D． | 3i |
分析 化简复数为a+bi的形式，即可求出z的虚部．
解答 解：复数z满足（4-3i）z=|3+4i|，
可得：（4+3i）（4-3i）z=|3+4i|（4+3i），
即25z=5（4+3i），
z=$\frac{4}{5}$+$\frac{3}{5}$i．
∴z的虚部为：$\frac{3}{5}$．
故选：B．
点评 本题考查复数的基本运算，复数的基本概念，是基础题．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
17．已知数列{an}共有n项，且通项公式为ak=k+3k（k∈N*），则数列{ak${C}_{n}^{k}$}的各项之和Sn为（ ）
| A． | n•4n-1 | B． | 4n-1 | C． | n•2n-1+4n-1 | D． | n•4n-1+2n-1 |
15．为普及高中生安全逃生知识与安全防护能力，雅礼中学高一年级举办了高中生安全知识与安全逃生能力竞赛．该竞赛分为预赛和决赛两个阶段，预赛为笔试，决赛为技能比赛．先将所有参赛选手参加笔试的成绩（得分均为整数，满分为100分）进行统计，制成如下频率分布表．
（1）求出上表中的x，y，z，s，p的值；
（2）按规定，预赛成绩不低于90分的选手参加决赛，参加决赛的选手按照抽签方式决定出场顺序．已知高一1401班恰有甲、乙两名同学取得决赛资格．记高一1401班在决赛中进入前三名的人数为X，求X的分布列和数学期望．（我们认为决赛中各选手的水平相当，获得各名次的机会均等）
| 分数（分数段） | 频数（人数） | 频率 |
| [60，70） | 9 | x |
| [70，80） | y | 0.38 |
| [80，90） | 16 | 0.32 |
| [90，100） | z | s |
| 合 计 | p | 1 |
（2）按规定，预赛成绩不低于90分的选手参加决赛，参加决赛的选手按照抽签方式决定出场顺序．已知高一1401班恰有甲、乙两名同学取得决赛资格．记高一1401班在决赛中进入前三名的人数为X，求X的分布列和数学期望．（我们认为决赛中各选手的水平相当，获得各名次的机会均等）
12．如图是某算法的程序框图，若程序运行后输出的结果是27，则判断框①处应填入的条件是（ ）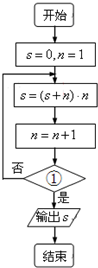
| A． | n＞2 | B． | n＞3 | C． | n＞4 | D． | n＞5 |
17．已知实数x，y满足平面区域$D：\left\{\begin{array}{l}x+y-1≥0\\ 2x-y-2≤0\\ x-2y+2≥0\end{array}\right.$，则x2+y2的最大值为（ ）
| A． | $\frac{1}{2}$ | B． | 1 | C． | $2\sqrt{2}$ | D． | 8 |