题目内容
15.为普及高中生安全逃生知识与安全防护能力,雅礼中学高一年级举办了高中生安全知识与安全逃生能力竞赛.该竞赛分为预赛和决赛两个阶段,预赛为笔试,决赛为技能比赛.先将所有参赛选手参加笔试的成绩(得分均为整数,满分为100分)进行统计,制成如下频率分布表.| 分数(分数段) | 频数(人数) | 频率 |
| [60,70) | 9 | x |
| [70,80) | y | 0.38 |
| [80,90) | 16 | 0.32 |
| [90,100) | z | s |
| 合 计 | p | 1 |
(2)按规定,预赛成绩不低于90分的选手参加决赛,参加决赛的选手按照抽签方式决定出场顺序.已知高一1401班恰有甲、乙两名同学取得决赛资格.记高一1401班在决赛中进入前三名的人数为X,求X的分布列和数学期望.(我们认为决赛中各选手的水平相当,获得各名次的机会均等)
分析 (1)利用比例关系直接求解所求数值即可.
(2)随机变量X的可能取值为0,1,2,求出概率,得到分布列,然后求解期望即可.
解答 解:(1)由题意知,9:x=16:0.32,解得x=0.18,同理可得y=19,z=6,s=0.12,
p=9+19+16+6=50----------4分
(2)由(1)知,参加决赛的选手共6人,--------------4分
随机变量X的可能取值为0,1,2--------------6分
$P(X=0)=\frac{A_3^2A_4^4}{A_6^6}=\frac{1}{5}$,
$P(X=1)=\frac{C_2^1A_3^1A_3^1A_4^4}{A_6^6}=\frac{3}{5}$,
$P(X=2)=\frac{A_3^2A_4^4}{A_6^6}=\frac{1}{5}$,--------------10分
随机变量X的分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
因为 $EX=0×\frac{1}{5}+1×\frac{3}{5}+2×\frac{1}{5}=1$,
所以随机变量X的数学期望为1.--------------12分.
点评 本题考查离散型随机变量的分布列,频率分布表的应用,考查计算能力.

练习册系列答案
相关题目
3.设x,y满足不等式组$\left\{{\begin{array}{l}{x+y-6≤0}\\{2x-y-1≤0}\\{3x-y-2≥0}\end{array}}\right.$,若z=ax+y的最大值为2a+4,最小值为a+1,则实数a的取值范围为( )
| A. | [-1,2] | B. | [-2,1] | C. | [-3,-2] | D. | [-3,1] |
20.执行如图所示的程序框图,若输出S=15,则框图中①处可以填入 ( )
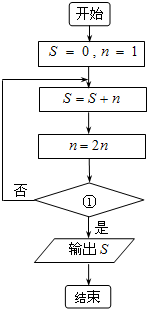

| A. | n≥4? | B. | n≥8? | C. | n≥16? | D. | n<16? |
7.若复数z满足(4-3i)z=|3+4i|,则z的虚部为( )
| A. | $\frac{3}{5}$i | B. | $\frac{3}{5}$ | C. | 3 | D. | 3i |
 .
.