题目内容
8.已知菱形ABCD与椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1相切,则菱形ABCD面积的最小值为( )| A. | 8$\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 8$\sqrt{3}$ |
分析 设菱形的边在第一象限所在直线的方程为:$\frac{x}{m}+\frac{y}{n}$=1,化为nx+my=mn(m,n>0).与椭圆方程联立化为(3m2+4n2)x2-8mn2x+4n2m2-12m2=0,令△=0,即可得出.
解答 解:设菱形的边在第一象限所在直线的方程为:$\frac{x}{m}+\frac{y}{n}$=1,化为nx+my=mn(m,n>0).
联立$\left\{\begin{array}{l}{nx+my=mn}\\{3{x}^{2}+4{y}^{2}=12}\end{array}\right.$,
化为(3m2+4n2)x2-8mn2x+4n2m2-12m2=0,
令△=64m2n4-16(3m2+4n2)(n2m2-3m2)=0,
化为m2n2=3m2+4n2≥2$\sqrt{3×4}$mn,当且仅当$\sqrt{3}m$=2n=$2\sqrt{6}$时取“=”.
解得mn≥4$\sqrt{3}$,
∴S菱形=$\frac{1}{2}×2m×2n$=2mn≥8$\sqrt{3}$.
∴菱形ABCD面积的最小值为8$\sqrt{3}$.
故选:D.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相切问题、菱形的面积计算公式、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
20.下列各图中,可表示函数y=f(x)的图象的只可能是( )
| A. | 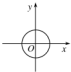 | B. | 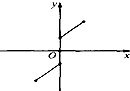 | C. | 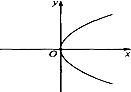 | D. | 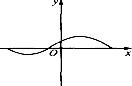 |
 已知函数f(x)=$\left\{\begin{array}{l}{x^2}+x,x<0\\{x^2}-x,x>0\end{array}$,
已知函数f(x)=$\left\{\begin{array}{l}{x^2}+x,x<0\\{x^2}-x,x>0\end{array}$,