题目内容
16．
已知函数f（x）=$\left\{\begin{array}{l}{x^2}+x，x＜0\\{x^2}-x，x＞0\end{array}$，（1）作出函数的图象；并写出单调区间．
（2）求函数的最小值，并求出对应的x的值．
分析 （1）根据函数的解析式，作出函数的图象，数形结合求得函数的单调区间．
（2）结合函数的图象，求得函数的最小值，并求出对应的x的值．
解答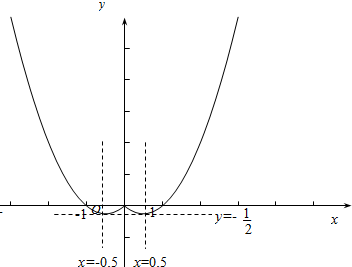 
解：（1）函数f（x）=$\left\{\begin{array}{l}{x^2}+x，x＜0\\{x^2}-x，x＞0\end{array}$ 的图象如图所示：
结合图象，可得函数的增区间为$（{-\frac{1}{2}，0}），（{\frac{1}{2}，+∞}）$，
减区间为$（{-∞，-\frac{1}{2}}），（{0，\frac{1}{2}}）$．
（2）结合图象可得 $f{（x）_{min}}=-\frac{1}{4}$，
此时对应的$x=±\frac{1}{2}$．
点评 本题主要考查函数的图象特征，函数的单调性以及最小值，体现了数形结合的数学思想，属于中档题．
练习册系列答案
相关题目
4．若直线x+（a-1）y+2=0和2x+3y+1=0互相垂直，则a=（ ）
| A． | $\frac{1}{3}$ | B． | -$\frac{2}{3}$ | C． | -$\frac{1}{3}$ | D． | $\frac{2}{3}$ |
1．在平面直角坐标系中，O为坐标原点，P是由不等式组$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{x+y≥1}\end{array}\right.$所确定的平面区域内的动点，点Q是直线3x+4y-7=0上任意一点，O为坐标原点，则|$\overline{OP}+\overline{OQ}$|的最小值为（ ）
| A． | $\frac{7}{5}$ | B． | 2 | C． | $\frac{9}{5}$ | D． | $\frac{11}{5}$ |
8．已知菱形ABCD与椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1相切，则菱形ABCD面积的最小值为（ ）
| A． | 8$\sqrt{2}$ | B． | 2$\sqrt{2}$ | C． | 2$\sqrt{3}$ | D． | 8$\sqrt{3}$ |
5．从空间一点出发的三条射线PA，PB，PC均成60°角，则二面角B-PA-C的大小为（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{π}{2}$ | C． | $arcsin\frac{1}{3}$ | D． | $arccos\frac{1}{3}$ |