题目内容
【题目】已知函数f(x) .
.

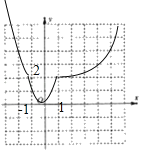
(1)画出函数f(x)的图象,根据图象直接写出f(x)的值域;
(2)根据图象直接写出满足f(x)≥2的所有x的集合;
(3)若f(x)的递减区间为(﹣∞,a),递增区间为(b,+∞),直接写出a的最大值,b的最小值.
【答案】(1)图见解析,值域为:[0,+∞);(2)(﹣∞,﹣1]∪[1,+∞);(3)a的最大值为0,b的最小值为0.
【解析】
(1)根据分段函数解析式,画出函数图象,并根据图象求得函数![]() 的值域.
的值域.
(2)根据图象,求得不等式![]() 的解集.
的解集.
(3)根据图象,由图求得函数![]() 的单调区间,进而求得
的单调区间,进而求得![]() 的最大值和
的最大值和![]() 的最小值.
的最小值.
(1)因为函数f(x)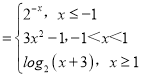 .
.
所以:函数f(x)的图象如图:;由图可知其值域为:[0,+∞);
(2)满足f(x)≥2的所有x的集合是:(﹣∞,﹣1]∪[1,+∞);
(3)因为函数的递减区间为:(﹣∞,0];递增区间为:[0,+∞);
f(x)的递减区间为(﹣∞,a),递增区间为(b,+∞)
∴a的最大值为0,b的最小值为0.

练习册系列答案
相关题目