Question

【题目】已知圆C：x2+y2﹣4y+1＝0，点M（﹣1，﹣1），从圆C外一点P向该圆引一条切线，记切点为T．

（1）若过点M的直线l与圆交于A，B两点且|AB|＝2，求直线l的方程；

（2）若满足|PT|＝|PM|，求使|PT|取得最小值时点P的坐标．

Answer 1

【答案】（1）x＝﹣1或4x﹣3y+1＝0；（2）（，）

【解析】

（1）首先判断斜率不存在时，符合题意.当斜率存在时，设出直线的方程，利用弦长列方程，解方程求得直线的斜率，进而求得直线方程.

（2）设出点的坐标，根据切线长以及列方程，化简后求得的轨迹方程，将最小转化为到直线的距离，求得垂直直线时直线的方程，和联立求得点坐标.

（1）圆C的标准方程为x2+（y﹣2）2＝3．

当直线l的斜率不存在时，直线l的方程为x＝﹣1，

此时|AB|＝2，满足题意；

当直线l的斜率存在时，设直线l的方程为y+1＝k（x+1），即kx﹣y+k﹣1＝0．

∵|AB|＝2，

∴圆心C到直线l的距离d1．

∴d1．

解得k，

则直线l的方程为4x﹣3y+1＝0．

∴所求直线l的方程为x＝﹣1或4x﹣3y+1＝0；

（2）设P（x0，y0），|PT|，

∵|PT|＝|PM|，∴，

化简得2x0+6y0+1＝0，

∴点P（x0，y0）在直线2x+6y+1＝0．

当|PT|取得最小值时，即|PM|取得最小值，

即为点M（﹣1，﹣1）到直线2x+6y+1＝0的距离，

此时直线PM垂直于直线2x+6y+1＝0，

∴直线PM的方程为6x﹣2y+4＝0，即3x﹣y+2＝0．

由 ，解得 ，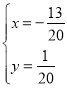

∴点P的坐标为（，）．