题目内容
7.已知F是抛物线x2=4y的焦点,直线y=kx-1与该抛物线交于第一象限内的零点A,B,若|AF|=3|FB|,则k的值是( )| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
分析 根据抛物线方程求出准线方程与焦点坐标,利用抛物线的定义表示出|AF|与|FB|,
再利用直线与抛物线方程组成方程组,结合根与系数的关系,求出k的值即可.
解答 解:如图所示,
抛物线方程为x2=4y,
∴p=2,准线方程为y=-1,焦点坐标为F(0,1);
设点A(x1,y1),B(x2,y2),
则|AF|=y1+$\frac{p}{2}$=y1+1,|FB|=y2+$\frac{p}{2}$=y2+1;
∵|AF|=3|FB|,
∴y1+1=3(y2+1),即y1=3y2+2;
联立方程组$\left\{\begin{array}{l}{y=kx-1}\\{{x}^{2}=4y}\end{array}\right.$,
消去x,得y2+(2-4k2)y+1=0,
由根与系数的关系得,y1+y2=4k2-2,
即(3y2+2)+y2=4k2-2,
解得y2=k2-1;
代入直线方程y=kx-1中,得x2=k,
再把x2、y2代入抛物线方程x2=4y中,
得k2=4k2-4,
解得k=$\frac{2\sqrt{3}}{3}$,或k=-$\frac{2\sqrt{3}}{3}$(不符合题意,应舍去),
∴k=$\frac{2\sqrt{3}}{3}$.
故选:D.
点评 本题考查了抛物线的标准方程与几何性质的应用问题,也考查了直线与抛物线的综合应用问题,考查了方程思想的应用问题,是综合性题目.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
16.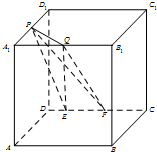 如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值b,则下面的四个值中不为定值的是( )
如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值b,则下面的四个值中不为定值的是( )
 如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值b,则下面的四个值中不为定值的是( )
如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值b,则下面的四个值中不为定值的是( )| A. | 点P到平面QEF的距离 | B. | 三棱锥P-QEF的体积 | ||
| C. | 直线PQ与平面PEF所成的角 | D. | 二面角P-EF-Q的大小 |
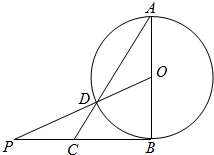 如图,AB为圆O的直径,O为圆心,PB与圆O相切于点B,PO交圆O于点D,AD的延长线交PB于点C,若AB=2,$PB=2\sqrt{2}$,则BC=$\sqrt{2}$.
如图,AB为圆O的直径,O为圆心,PB与圆O相切于点B,PO交圆O于点D,AD的延长线交PB于点C,若AB=2,$PB=2\sqrt{2}$,则BC=$\sqrt{2}$.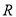 的函数
的函数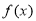 满足:
满足: .若
.若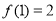 ,则
,则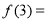 ________.
________.