题目内容
20.设等差数列{an}的前n项和为Sn,已知a7=4,a19=2a3.数列{bn}的前n项和为Tn.满足${4}^{2{a}_{n}-1}$=λTn-(a3-1)(n∈N*).(1)问是否存在非零实数λ,使得数列{bn}为等比数列?并说明理由;
(2)已知对于n∈N*,不等式$\frac{1}{{S}_{1}}$$+\frac{1}{{S}_{2}}+\frac{1}{{S}_{3}}+…+\frac{1}{{S}_{n}}$<M恒成立,求实数M的最小值.
分析 (1)通过a7=4、a19=2a3可得公差和首项,利用${4}^{2{a}_{n}-1}$=λTn-(a5-1)可得b1=$\frac{6}{λ}$、bn=$\frac{3}{λ}$4n-1(n≥2),比较后可得结论;
(2)通过对$\frac{1}{{S}_{n}}$分离分母,并项相加即得结论.
解答 解:(1)结论:不存在非零实数λ,使得数列{bn}为等比数列.
理由如下:
设等差数列{an}的公差为d,则an=a1+(n-1)d.
∵a7=4、a19=2a3,∴a1+6d=4、a1+18d=2(a1+2d),
解得a1=1,d=$\frac{1}{2}$,∴an=$\frac{n+1}{2}$,
∵a5=3,${4}^{2{a}_{n}-1}$=λTn-(a5-1),
∴4n=λTn-2,∴Tn=$\frac{1}{λ}$4n+$\frac{2}{λ}$.
当n=1时,b1=$\frac{6}{λ}$;
当n≥2时,bn=Tn-Tn-1=$\frac{1}{λ}$4n+$\frac{2}{λ}$-$\frac{1}{λ}$4n-1-$\frac{2}{λ}$=$\frac{3}{λ}$4n-1,
∴bn+1=4bn(n≥2),若{bn}是等比数列,则有b2=4b1,
而b1+b2=$\frac{18}{λ}$,b2=$\frac{12}{λ}$,∴$\frac{{b}_{2}}{{b}_{1}}$=2与b2=4b1矛盾,
故不存在非零实数λ,使得数列{bn}为等比数列;
(2)∵Sn=$\frac{n(n+3)}{4}$,∴$\frac{1}{{S}_{n}}$=$\frac{4}{n(n+3)}$=$\frac{4}{3}$($\frac{1}{n}$-$\frac{1}{n+3}$),
∴$\frac{1}{{S}_{1}}$$+\frac{1}{{S}_{2}}+\frac{1}{{S}_{3}}+…+\frac{1}{{S}_{n}}$
=$\frac{4}{3}$[$\frac{1}{1}$-$\frac{1}{4}$+$\frac{1}{2}$-$\frac{1}{5}$+$\frac{1}{3}$-$\frac{1}{6}$+$\frac{1}{4}$-$\frac{1}{7}$+…+$\frac{1}{n-2}$-$\frac{1}{n+1}$+$\frac{1}{n-1}$-$\frac{1}{n+2}$+$\frac{1}{n}$-$\frac{1}{n+3}$]
=$\frac{4}{3}$($\frac{1}{1}$+$\frac{1}{2}$+$\frac{1}{3}$-$\frac{1}{n+1}$-$\frac{1}{n+2}$-$\frac{1}{n+3}$)
=$\frac{4}{3}$($\frac{11}{6}$-$\frac{1}{n+1}$-$\frac{1}{n+2}$-$\frac{1}{n+3}$)
<$\frac{22}{9}$,
∴M≥$\frac{22}{9}$,即实数M的最小值为$\frac{22}{9}$.
点评 本题考查求数列的通项,判定数列和的取值范围,分离分母、并项相加是解决本题的关键,注意解题方法的积累,属于中档题.

| A. | $\frac{16\sqrt{6}}{3}$ | B. | 8 | C. | $\frac{5\sqrt{15}}{3}$ | D. | 6 |
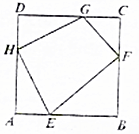 设四边形EFGH的四条边长为a,b,c,d,其四个顶点分别在单位正方形ABCD的四条边上,则2a2+b2+2c2+d2的最小值为( )
设四边形EFGH的四条边长为a,b,c,d,其四个顶点分别在单位正方形ABCD的四条边上,则2a2+b2+2c2+d2的最小值为( )| A. | 3 | B. | 6 | C. | $3\sqrt{2}$ | D. | $\frac{8}{3}$ |
| A. | 6 | B. | -6 | C. | -$\frac{1}{6}$ | D. | $\frac{1}{6}$ |
| A. | 2 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
 ,如果
,如果 ,那么
,那么 等于( )
等于( ) 值为___________.
值为___________.