题目内容
10. 已知三棱柱ABC-A1B1C1中,AB=BC=BB1,AB⊥BC,BB1⊥平面ABC,D为AC的中点,E为CC1的中点.
已知三棱柱ABC-A1B1C1中,AB=BC=BB1,AB⊥BC,BB1⊥平面ABC,D为AC的中点,E为CC1的中点.(1)求证AC1∥平面BDE;
(2)求证:AC1⊥平面A1BD.
分析 (1)由已知根据中位线定理可得DE∥AC1,又DE?平面BDE,AC1?平面BDE,由线面平行的判定定理即可证明.
(2)D为AC的中点,可证∠AA1D=∠CAC1,∠CAC1+∠ADA1=90°,从而可得AC1⊥A1D,又AC1⊥BD,即可证明AC1⊥平面A1BD.
解答 证明:(1)∵D为AC的中点,E为CC1的中点,
∴DE∥AC1,又DE?平面BDE,AC1?平面BDE,
∴AC1∥平面BDE;…6分
(2)D为AC的中点,则tan∠AA1D=$\frac{AD}{A{A}_{1}}=\frac{\sqrt{2}}{2}$,tan$∠CA{C}_{1}=\frac{C{C}_{1}}{AC}=\frac{\sqrt{2}}{2}$,
则∠AA1D=∠CAC1,那么∠CAC1+∠ADA1=90°,AC1⊥A1D,
又AC1⊥BD,所以AC1⊥平面A1BD…12分
点评 本题主要考查了直线与平面平行的判定,直线与平面垂直的判定,考查了空间想象能力和推理论证能力,属于中档题.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
1.函数y=x3与y=${(\frac{1}{2})^{x-2}}$图形的交点为(a,b),则a所在区间是( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
18.已知实数-1,x,y,z,-4成等比数列,则xyz=( )
| A. | -8 | B. | ±8 | C. | $-2\sqrt{2}$ | D. | $±2\sqrt{2}$ |
5.在等差数列{an}中,a1+a3=10,a4+a6=4,则公差d的值为( )
| A. | 1 | B. | 2 | C. | -2 | D. | -1 |
15.设公比为q的等比数列{an}中,an>0,且a1,$\frac{1}{2}$a3,2a2成等差数列,则q=( )
| A. | 1+$\sqrt{2}$ | B. | 1-$\sqrt{2}$ | C. | 1 | D. | $\sqrt{2}$ |
2.已知函数$f(x)=ln({1-\frac{a}{x+1}})(a∈R)$.命题p:?a∈R,f(x)是奇函数;命题q:?a∈R,f(x)在定义域内是增函数,那么下列命题为真命题的是( )
| A. | ?p | B. | p∧q | C. | (?p)∧q | D. | p∧(?q) |
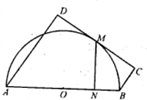 如图,AB为圆O的直径,直线CD与圆O相切于M,AD垂直CD于D,BC⊥CD于C,MN⊥AB于N,又AD=3,BC=1,则MN=$\sqrt{3}$.
如图,AB为圆O的直径,直线CD与圆O相切于M,AD垂直CD于D,BC⊥CD于C,MN⊥AB于N,又AD=3,BC=1,则MN=$\sqrt{3}$.