题目内容
1.函数y=x3与y=${(\frac{1}{2})^{x-2}}$图形的交点为(a,b),则a所在区间是( )| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
分析 构造函数f(x))=x3-${(\frac{1}{2})^{x-2}}$,根据函数零点和方程之间的关系判断函数零点的取值范围是解决本题的关键.
解答 解:∵y=x3与y=${(\frac{1}{2})^{x-2}}$,
∴设f(x)=x3-${(\frac{1}{2})^{x-2}}$,
则函数f(x)为增函数,
∵f(1)=1-$(\frac{1}{2})^{-1}$=1-2=-1<0,f(2)=${2}^{3}-(\frac{1}{2})^{2-2}=8-1=7$>0,
∴函数f(x)的根x∈(1,2),
∵函数y=x3与y=${(\frac{1}{2})^{x-2}}$图形的交点为(a,b),
∴a∈(1,2),
故选:B.
点评 本题主要考查函数零点的取值范围的应用,根据函数零点和方程之间的关系,构造函数是解决本题的关键.

练习册系列答案
相关题目
13.设a∈R,则“a=-1”是“f(x)=|(ax-2)x|在(0,+∞)上单调递增”的( )
| A. | 充要条件 | B. | 既不充分也不必要条件 | ||
| C. | 充分不必要条件 | D. | 必要不充分条件 |
 如图,AB、AC是⊙O的两条切线,切点分别为B、C.若∠BAC=60°,BC=6,则⊙O的半径为2$\sqrt{3}$.
如图,AB、AC是⊙O的两条切线,切点分别为B、C.若∠BAC=60°,BC=6,则⊙O的半径为2$\sqrt{3}$. 如图,点C是以AB为直径的圆O上不与A、B重合的一个动点,S是圆O所在平面外一点,且总有SC⊥平面ABC,M是SB的中点,AB=SC=2.
如图,点C是以AB为直径的圆O上不与A、B重合的一个动点,S是圆O所在平面外一点,且总有SC⊥平面ABC,M是SB的中点,AB=SC=2.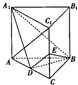 已知三棱柱ABC-A1B1C1中,AB=BC=BB1,AB⊥BC,BB1⊥平面ABC,D为AC的中点,E为CC1的中点.
已知三棱柱ABC-A1B1C1中,AB=BC=BB1,AB⊥BC,BB1⊥平面ABC,D为AC的中点,E为CC1的中点.