题目内容

20．设等差数列{an}的前n项和为An，等比数列{bn}的前n项和为Bn，若a3=b3，a4=b4，且$\frac{{A}_{5}-{A}_{3}}{{B}_{4}-{B}_{2}}$=7，则$\frac{{a}_{5}+{a}_{3}}{{b}_{5}+{b}_{3}}$=-$\frac{4}{5}$．

分析 由题意a3=b3，a4=b4，所以$\frac{2{a}_{1}+7d}{2{a}_{1}+5d}$=7，可得a1=-$\frac{7}{3}$d，求出数列{bn}的公比，即可得出结论．

解答 解：由题意，$\frac{{{A_5}-{A_3}}}{{{B_4}-{B_2}}}=7$=$\frac{{a}_{4}+{a}_{5}}{{b}_{3}+{b}_{4}}$，
因为a3=b3，a4=b4，
所以$\frac{2{a}_{1}+7d}{2{a}_{1}+5d}$=7，
所以a1=-$\frac{7}{3}$d，
所以数列{bn}的公比q=$\frac{{a}_{4}}{{a}_{3}}$=$\frac{{a}_{1}+3d}{{a}_{1}+2d}$=-2，
所以$\frac{{a}_{5}+{a}_{3}}{{b}_{5}+{b}_{3}}$=$\frac{2{a}_{1}+6d}{（{a}_{1}+2d）（4+1）}$=-$\frac{4}{5}$．
故答案为：-$\frac{4}{5}$．

点评 本题考查等差数列与等比数列的通项，考查学生的计算能力，比较基础．

练习册系列答案
相关题目
15．下列函数中，既是偶函数又在（0，+∞）上单调递增的是（　　）
A．y=|x+2|B．y=|x|+2C．y=-x2+2D．$y={（{\frac{1}{2}}）^{|x|}}$
11．已知函数f（x）=x3+mx2-m2x+2，g（x）=alnx，a、m∈R．
（1）若m＜0时，试求函数y=f（x）的单调递减区间；
（2）若对任意x∈[1，e]，都有g（x）≥-x2+（a+2）x恒成立，求a的取值范围．
8．已知命题“?x0∈R，x02+ax0-4a＜0”为假命题，则实数a的取值范围为（　　）
A．[-16，0]B．（-16，0）C．[-4，0]D．（-4，0）
15．设等差数列{an}的前n项和为An，等比数列{bn}的前n项和为Bn，若a3=b3，a4=b4，且$\frac{{{A_5}-{A_3}}}{{{B_4}-{B_2}}}=7$，则数列{bn}的公比q=-2．
5．集合A={0，2，a}，B={a2}，若A∪B=A，则a的值有（　　）
A．1个B．2个C．3个D．4个
12．已知函数$f（x）={（\sqrt{x}+\sqrt{2}）^2}$，（x≥0），又数列{an}中，an＞0，a1=2，该数列的前n项和记为Sn，对所有大于1的自然数n都有Sn=f（Sn-1）．
（Ⅰ）求{an}的通项公式；
（Ⅱ）记bn=$\frac{{{a_{n+1}}^2+{a_n}^2}}{{2{a_{n+1}}{a_n}}}$，{bn}其前n项和为Tn，证明：Tn＜n+1．
9．如图，AB、AC是⊙O的两条切线，切点分别为B、C．若∠BAC=60°，BC=6，则⊙O的半径为2$\sqrt{3}$．
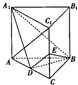10．已知三棱柱ABC-A1B1C1中，AB=BC=BB1，AB⊥BC，BB1⊥平面ABC，D为AC的中点，E为CC1的中点．
（1）求证AC1∥平面BDE；
（2）求证：AC1⊥平面A1BD．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网