题目内容
2.已知函数$f(x)=ln({1-\frac{a}{x+1}})(a∈R)$.命题p:?a∈R,f(x)是奇函数;命题q:?a∈R,f(x)在定义域内是增函数,那么下列命题为真命题的是( )| A. | ?p | B. | p∧q | C. | (?p)∧q | D. | p∧(?q) |
分析 判定命题p、q的真假,再根据复合命题真值表可得答案.
解答 解:存在a=0,f(x)=ln(1-$\frac{a}{x+1}$)=ln1=0既是奇函数又是偶函数,
也存在a=2,使f(x)=ln(1-$\frac{a}{x+1}$)=ln(1-$\frac{2}{x+1}$)=ln($\frac{x-1}{x+1}$),
因为f(-x)=ln($\frac{-x-1}{-x+1}$)=ln($\frac{x+1}{x-1}$)=-f(x)此时函数f(x)是奇函数,所以命题p为真命题,¬p为假命题,
而当a=0,f(x)=ln(1-$\frac{a}{x+1}$)=ln1=0没有单调性,所以命题q为假命题,¬q为真命题,
故p∧(?q)为真命题,
故选:D.
点评 本题借助考查复合命题的真假判断,考查了函数的奇偶性及单调质,解题的关键是熟练掌握复合命题的真假规律.

练习册系列答案
相关题目
13.设a∈R,则“a=-1”是“f(x)=|(ax-2)x|在(0,+∞)上单调递增”的( )
| A. | 充要条件 | B. | 既不充分也不必要条件 | ||
| C. | 充分不必要条件 | D. | 必要不充分条件 |
17.若变量x,y满足约束条件$\left\{\begin{array}{l}{y≤0}\\{x-2y≥1}\\{x-4y≤3}\end{array}\right.$,则z=3x+5y的最小值为( )
| A. | 9 | B. | -9 | C. | -8 | D. | 8 |
14.复数z=$\frac{2l}{1+i}$(i是虚数单位)是( )
| A. | 1-i | B. | 1+i | C. | -1+i | D. | -1-i |
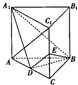 已知三棱柱ABC-A1B1C1中,AB=BC=BB1,AB⊥BC,BB1⊥平面ABC,D为AC的中点,E为CC1的中点.
已知三棱柱ABC-A1B1C1中,AB=BC=BB1,AB⊥BC,BB1⊥平面ABC,D为AC的中点,E为CC1的中点.