题目内容
19. 如图,AB为圆O的直径,直线CD与圆O相切于M,AD垂直CD于D,BC⊥CD于C,MN⊥AB于N,又AD=3,BC=1,则MN=$\sqrt{3}$.
如图,AB为圆O的直径,直线CD与圆O相切于M,AD垂直CD于D,BC⊥CD于C,MN⊥AB于N,又AD=3,BC=1,则MN=$\sqrt{3}$.
分析 连接AM,OM,BM,证明△CMB≌△NMB,可得CM=NM,再求出CD,即可求出MN.
解答  解:连接AM,OM,BM,则
解:连接AM,OM,BM,则
因为直线CD与圆O相切于M,
所以∠CMB=∠MAM,
因为AB为圆O的直径,MN⊥AB,
所以∠NMB=∠MAM,
所以∠CMB=∠NMB,
因为BC⊥CD于C,MN⊥AB,
所以△CMB≌△NMB,
所以CM=NM,
因为直线CD与圆O相切于M,AD垂直CD于D,BC⊥CD于C,AD=3,BC=1,
所以OM=2,
所以AB=4,
所以CD=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
所以CM=$\sqrt{3}$
所以MN=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查三角形全等的证明,考查圆的切线的性质,属于中档题.

练习册系列答案
相关题目
14.复数z=$\frac{2l}{1+i}$(i是虚数单位)是( )
| A. | 1-i | B. | 1+i | C. | -1+i | D. | -1-i |
8.下列三个数:a=ln$\frac{3}{2}$-$\frac{3}{2}$,b=lnπ-π,c=ln3-3,大小顺序正确的是( )
| A. | a>c>b | B. | a>b>c | C. | a<c<b | D. | b>a>c |
 如图,AB、AC是⊙O的两条切线,切点分别为B、C.若∠BAC=60°,BC=6,则⊙O的半径为2$\sqrt{3}$.
如图,AB、AC是⊙O的两条切线,切点分别为B、C.若∠BAC=60°,BC=6,则⊙O的半径为2$\sqrt{3}$.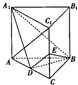 已知三棱柱ABC-A1B1C1中,AB=BC=BB1,AB⊥BC,BB1⊥平面ABC,D为AC的中点,E为CC1的中点.
已知三棱柱ABC-A1B1C1中,AB=BC=BB1,AB⊥BC,BB1⊥平面ABC,D为AC的中点,E为CC1的中点. 将边长为2的等边△ABC沿x轴正方向滚动,某时刻A与坐标原点重合(如图),设顶点A(x,y)的轨迹方程是y=f(x),关于函数y=f(x)有下列说法:
将边长为2的等边△ABC沿x轴正方向滚动,某时刻A与坐标原点重合(如图),设顶点A(x,y)的轨迹方程是y=f(x),关于函数y=f(x)有下列说法: