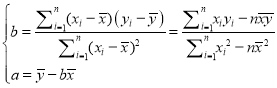题目内容
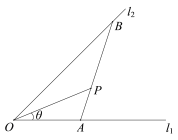
【题目】如图,某地村庄P与村庄O的距离为![]() 千米,从村庄O出发有两条道路
千米,从村庄O出发有两条道路![]() ,经测量,
,经测量,![]() 的夹角为
的夹角为![]() ,OP与
,OP与![]() 的夹角
的夹角![]() 满足
满足![]() (其中
(其中![]() ),现要经过P修一条直路分别与道路
),现要经过P修一条直路分别与道路![]() 交汇于
交汇于![]() 两点,并在
两点,并在![]() 处设立公共设施.
处设立公共设施.
(1)已知修建道路![]() 的单位造价分别为2m元/千米和m元/千米,若两段道路的总造价相等,求此时点
的单位造价分别为2m元/千米和m元/千米,若两段道路的总造价相等,求此时点![]() 之间的距离;
之间的距离;
(2)考虑环境因素,需要对![]() 段道路进行翻修,
段道路进行翻修,![]() 段的翻修单价分别为n元/千米和
段的翻修单价分别为n元/千米和![]() 元/千米,要使两段道路的翻修总价最少,试确定
元/千米,要使两段道路的翻修总价最少,试确定![]() 点的位置.
点的位置.
【答案】(1)![]() 千米; (2)A位于距O点3千米处,B位于距O点3千米处..
千米; (2)A位于距O点3千米处,B位于距O点3千米处..
【解析】
(1)先建立坐标系,求出P点坐标,再根据条件求B点坐标,最后根据两点间距离公式得结果,(2)先设直线![]() 方程,解得A,B坐标,用坐标表示翻修总价,最后利用导数求函数最值.
方程,解得A,B坐标,用坐标表示翻修总价,最后利用导数求函数最值.
(1)以O为原点,直线OA为x轴建立平面直角坐标系,
因为![]() ,所以
,所以![]() ,
,
设![]() ,由
,由![]() ,得
,得![]() ,所以
,所以![]() .
.
由题意得![]() ,所以
,所以![]() ,所以B点纵坐标为
,所以B点纵坐标为![]() ,
,
又因为点B在直线![]() 上,所以
上,所以![]() ,
,
所以![]() .
.
答:![]() 之间的距离为
之间的距离为![]() 千米.
千米.
(2)设总造价为S,则![]() ,
,
设![]() ,要使S最小,只要y最小.
,要使S最小,只要y最小.
当![]() 轴时,
轴时,![]() ,这时
,这时![]() ,
,
所以![]() .
.
当AB与x轴不垂直时,设直线![]() 方程为
方程为![]() ,
,
令![]() ,得点A的横坐标为
,得点A的横坐标为![]() ,所以
,所以![]() ,
,
令![]() ,得点B的横坐标为
,得点B的横坐标为![]() ,
,![]() ,
,
因为![]() 且
且![]() ,所以
,所以![]() 或
或![]() ,
,
此时![]() ,
,
![]() ,
,
当![]() 时,y在
时,y在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
所以![]() ,此时
,此时![]() ;
;
当![]() 时,
时,![]() .
.
综上所述,要使![]() 段道路的翻修总价最少,A位于距O点3千米处,B位于距O点
段道路的翻修总价最少,A位于距O点3千米处,B位于距O点![]() 千米处.
千米处.
答:要使![]() 段道路的翻修总价最少,A位于距O点3千米处,B位于距O点3千米处.
段道路的翻修总价最少,A位于距O点3千米处,B位于距O点3千米处.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案【题目】为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
喜爱打篮球 | 不喜爱打篮球 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有99%的把握认为“喜爱打篮球与性别有关”?说明你的理由.
参考公式:独立性检测中,随机变量![]() ,
,
其中![]() 为样本容量
为样本容量
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据
(吨)标准煤的几组对照数据
|
|
|
|
|
|
|
|
|
|
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
参考公式: