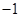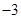题目内容
(满分16分)已知函数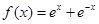 ,其中
,其中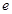 是自然对数的底数.
是自然对数的底数.
(1)证明: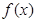 是
是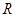 上的偶函数;
上的偶函数;
(2)若关于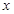 的不等式
的不等式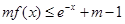 在
在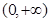 上恒成立,求实数
上恒成立,求实数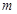 的取值范围;
的取值范围;
(3)已知正数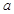 满足:存在
满足:存在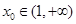 ,使得
,使得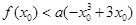 成立,试比较
成立,试比较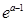 与
与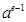 的大小,并证明你的结论.
的大小,并证明你的结论.
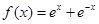 ,其中
,其中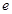 是自然对数的底数.
是自然对数的底数.(1)证明:
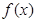 是
是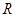 上的偶函数;
上的偶函数;(2)若关于
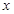 的不等式
的不等式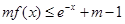 在
在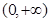 上恒成立,求实数
上恒成立,求实数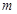 的取值范围;
的取值范围;(3)已知正数
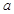 满足:存在
满足:存在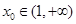 ,使得
,使得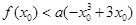 成立,试比较
成立,试比较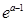 与
与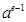 的大小,并证明你的结论.
的大小,并证明你的结论.(1)证明见解析;(2)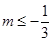 ;(3)当
;(3)当 时,
时,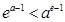 ,当
,当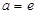 时,
时,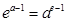 ,当
,当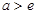 时,
时,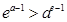 .
.
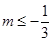 ;(3)当
;(3)当 时,
时,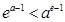 ,当
,当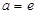 时,
时,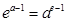 ,当
,当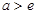 时,
时,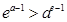 .
.试题分析:
试题解析:(1)证明:函数
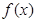 定义域为
定义域为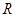 ,∵
,∵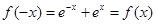 ,∴
,∴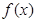 是偶函数.
是偶函数.(2)由
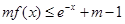 得
得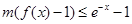 ,由于当
,由于当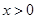 时,
时,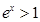 ,因此
,因此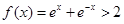 ,即
,即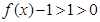 ,所以
,所以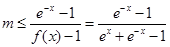
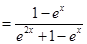 ,令
,令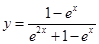 ,设
,设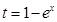 ,则
,则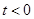 ,
,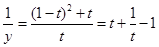 ,∵
,∵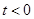 ,∴
,∴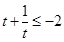 (
(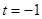 时等号成立),即
时等号成立),即 ,
,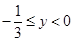 ,所以
,所以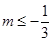 .
.(3)由题意,不等式
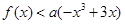 在
在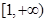 上有解,由
上有解,由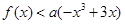 得
得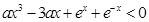 ,记
,记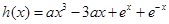 ,
, ,显然
,显然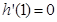 ,当
,当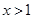 时,
时,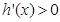 (因为
(因为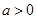 ),故函数
),故函数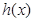 在
在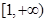 上增函数,
上增函数,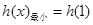 ,于是
,于是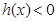 在
在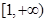 上有解,等价于
上有解,等价于 ,即
,即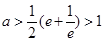 .考察函数
.考察函数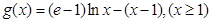 ,
,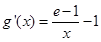 ,当
,当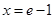 时,
时,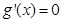 ,当
,当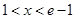 时,
时,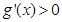 ,当
,当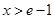 时
时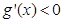 ,即
,即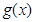 在
在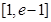 上是增函数,在
上是增函数,在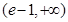 上是减函数,又
上是减函数,又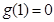 ,
,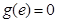 ,
, ,所以当
,所以当 时,
时,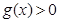 ,即
,即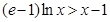 ,
, ,当
,当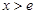 时,
时,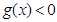 ,,即
,,即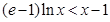 ,
,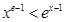 ,因此当
,因此当 时,
时,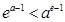 ,当
,当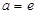 时,
时,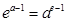 ,当
,当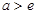 时,
时,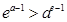 .
.【考点】(1)偶函数的判断;(2)不等式恒成立问题与函数的交汇;(3)导数与函数的单调性,比较大小.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
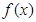 是定义在区间-2,2上的偶函数,当
是定义在区间-2,2上的偶函数,当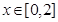 时,
时,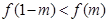 成立,则实数
成立,则实数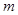 的取值范围( )
的取值范围( )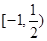
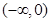
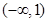
 是R上的偶函数,若将
是R上的偶函数,若将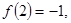 则
则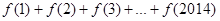 =( )
=( )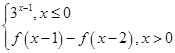 ,则f(2 016)=________.
,则f(2 016)=________.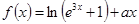 是偶函数,则
是偶函数,则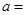 ____________.
____________.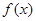 是周期为4的奇函数,当
是周期为4的奇函数,当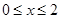 时,
时,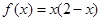 ,则
,则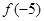 等于 ( )
等于 ( )