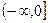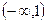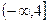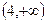题目内容
证明关于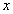 的不等式
的不等式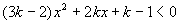 与
与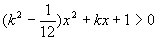 ,当
,当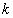 为任意实数时,至少有一个桓成立。
为任意实数时,至少有一个桓成立。
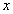 的不等式
的不等式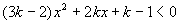 与
与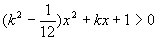 ,当
,当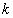 为任意实数时,至少有一个桓成立。
为任意实数时,至少有一个桓成立。答案见解析
证明不等式恒成立,实质是证明对应抛物线恒在 轴的上方或下方的问题,故只要求抛物线恒在
轴的上方或下方的问题,故只要求抛物线恒在 轴上方或下方的充要条件即可。
轴上方或下方的充要条件即可。
即由 恒成立
恒成立 对应抛物线恒在
对应抛物线恒在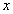 轴下方
轴下方
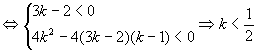 ;
;
由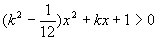 恒成立
恒成立 对应抛物线恒在
对应抛物线恒在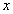 轴上方
轴上方
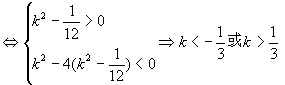 。
。
因此,当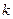 为任意实教时,上述两充要条件至少有一个成立,命题得证。
为任意实教时,上述两充要条件至少有一个成立,命题得证。
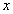 轴的上方或下方的问题,故只要求抛物线恒在
轴的上方或下方的问题,故只要求抛物线恒在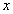 轴上方或下方的充要条件即可。
轴上方或下方的充要条件即可。即由
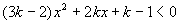 恒成立
恒成立 对应抛物线恒在
对应抛物线恒在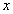 轴下方
轴下方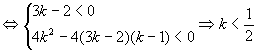 ;
;由
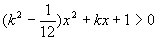 恒成立
恒成立 对应抛物线恒在
对应抛物线恒在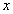 轴上方
轴上方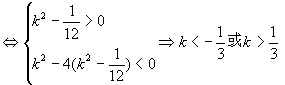 。
。因此,当
 为任意实教时,上述两充要条件至少有一个成立,命题得证。
为任意实教时,上述两充要条件至少有一个成立,命题得证。 
练习册系列答案
相关题目
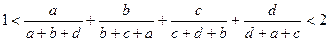
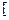 -2,2
-2,2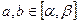 ,求证:
,求证: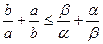
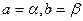 或
或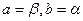 成立,
成立,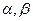 为正实数.
为正实数.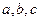 为互不相等的正数,
为互不相等的正数,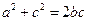 ,则下列关系中可能成立的是( )
,则下列关系中可能成立的是( )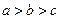
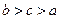
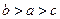
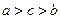
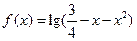 ,则
,则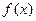 的单调递减区间是 。
的单调递减区间是 。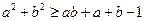
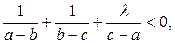 对满足
对满足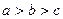 恒成立,则
恒成立,则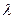 的取值范围是( )
的取值范围是( )