题目内容
(本小题满分14分)设实数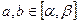 ,求证:
,求证: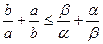
其中等号当且仅当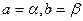 或
或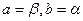 成立,
成立,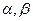 为正实数.
为正实数.
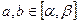 ,求证:
,求证: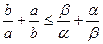
其中等号当且仅当
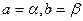 或
或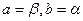 成立,
成立,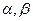 为正实数.
为正实数.略
:由对称性,不妨设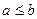 ,令
,令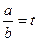 ,则因
,则因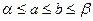 ,可得
,可得 (3分)
(3分)
设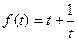
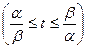 ,则对
,则对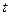 求导,得
求导,得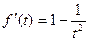 .…………(6分)
.…………(6分)
易知,当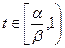 时,
时,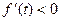 ,
,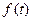 单调递减;当
单调递减;当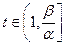 时,
时,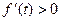 ,
,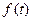 单调递增.…(9分)
单调递增.…(9分)
故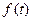 在
在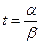 或
或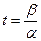 处有最大值且
处有最大值且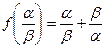 及
及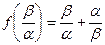 两者相等.
两者相等.
故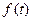 的最大值为
的最大值为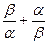 ,即
,即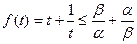 .………………(12分)
.………………(12分)
由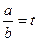 ,得
,得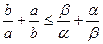 ,其中等号仅当
,其中等号仅当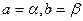 或
或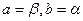 成立.………(14分)
成立.………(14分)
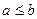 ,令
,令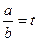 ,则因
,则因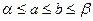 ,可得
,可得 (3分)
(3分)设
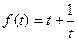
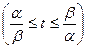 ,则对
,则对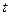 求导,得
求导,得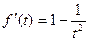 .…………(6分)
.…………(6分)易知,当
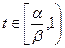 时,
时,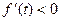 ,
,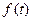 单调递减;当
单调递减;当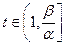 时,
时,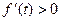 ,
,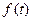 单调递增.…(9分)
单调递增.…(9分)故
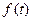 在
在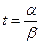 或
或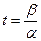 处有最大值且
处有最大值且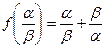 及
及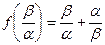 两者相等.
两者相等.故
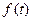 的最大值为
的最大值为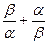 ,即
,即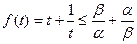 .………………(12分)
.………………(12分)由
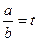 ,得
,得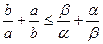 ,其中等号仅当
,其中等号仅当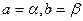 或
或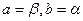 成立.………(14分)
成立.………(14分)
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
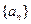 满足
满足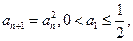 求证:
求证: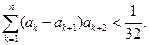
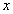 的不等式
的不等式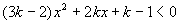 与
与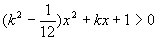 ,当
,当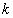 为任意实数时,至少有一个桓成立。
为任意实数时,至少有一个桓成立。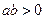 ;②
;②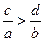 ;③
;③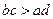 ,以其中两个作为条件,余下一个作结论,则可组成几个正确命题.
,以其中两个作为条件,余下一个作结论,则可组成几个正确命题.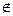 R+,且x+4y=1,则xy的最大值为 .
R+,且x+4y=1,则xy的最大值为 .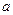 ,b是两个实数,且
,b是两个实数,且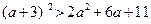 ;②
;②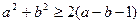 ;③
;③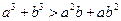 ;④
;④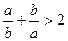 。上述4个式子中恒成立的有 ( )
。上述4个式子中恒成立的有 ( )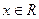 ,
,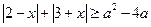 恒成立,则
恒成立,则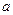 的取值范围是
的取值范围是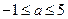 B.
B. 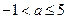 C.
C. 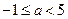 D.
D.